2024.01.20
「a = a + 1」とは？
はじめに
プログラムを作らない人にとって「a = a + 1」という式は、aを求める方程式です。
「a」と「a+1」の間に「=」(等しい、イコール)があるので、「a = a + 1」は「aと(a+1)は等しい」となります。
以下に書いた式のように「=」の両辺の値が等しいと考えるのは正しいことです。
3 = 3 10 = 5 × 2 6 ÷ 2 = 1 ＋ 2 a = a a × 0 = 0
方程式「a = a + 1」を解いてみる
それでは、「a = a + 1」を満たすaが有るのか、実際に解いてみましょう。
解き方は、まず右辺のaを左辺に移行して左辺にaをまとめます。
この場合は、「=」の左と右の両方からaを引くと考えても良いです。
a = a + 1 … 元の式 a - a = 1 … 右辺のaを左辺に移行
次に、左辺のa-aを計算します。
0 = 1 … 左辺のa - aを計算
aの方程式を解いた結果、 両方の辺からaがなくなり「解なし」となりました。
「a = a + 1」だけではなく、「a = a + 3」や「a = a - 10」などの方程式も同様に「解なし」となります。
ソースコードの中の「a = a + 1」
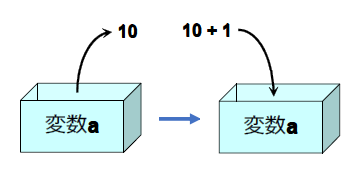
a ← a + 1
例えば、a = 10の場合に「a = a + 1」の処理が実行されると、a = 11となります。
プログラミング言語によって違いますが、Pascalという言語では代入を表す「a = a + 1」を
a := a + 1
と書きます。値の代入に「=」を使わずに「:=」を使います。
この書き方だと方程式に見えないので、代入と区別がつきやすいかもしれないです。
足し算(+)以外の計算
一般的なプログラミング言語では、「a = a + 1」は、a + 1をaに代入することを表しています。
「a = a - 3」、「a = a * 5」、「a = a / 10」、「a = a * 10 + 3」などの式はどうでしょうか？
「a = a - 3」は、a - 3をaに代入することを表しています。
「a = a * 5」は、aを5倍した値をaに代入することを表しています。
「a = a / 10」は、aを10で割った値をaに代入することを表しています。
「a = a * 10 + 3」は、aを10倍した値に3を足した値をaに代入することを表しています。
このように足し算(+)以外の右辺の計算値を左辺に代入します。
a * 5 = a + 6 … 左辺が変数名だけになっていない a / 2 = a * 9 … 左辺が変数名だけになっていない 0 = a + 1 … 数字だけの変数名は使えません 100 = a * 1 + a … 数字だけの変数名は使えません
変数の名前の付け方のルールは、以下の記事を参考にしてください。
以上です。
関連コンテンツ
割り算で「割り切れる」、「割り切れない」ってどういうこと？
広告
