2024.5.16
tan(タンジェント)
はじめに
ここでは、Math.tanメソッドを使わずに、Math.cosメソッドとMath.sinメソッドを使ってtanθを計算する方法を解説します。
Math.cos、Math.sinメソッドの仕様は以下のとおりで、角度をラジアンで渡すとそれぞれの値が戻ってきます。
Math.sinメソッド
public static double Math.sin( double a )
・引数aで指定した角度の正弦 (サイン) を返します。 パラメータ a : ラジアンで指定した角度。 戻り値 aの正弦
Math.cosメソッド
public static double Math.cos( double a )
・引数aで指定した角度の余弦 (コサイン) を返します。 パラメータ a : ラジアンで指定した角度。 戻り値 aの余弦
sinθとcosθを使ってtanθを求める方法
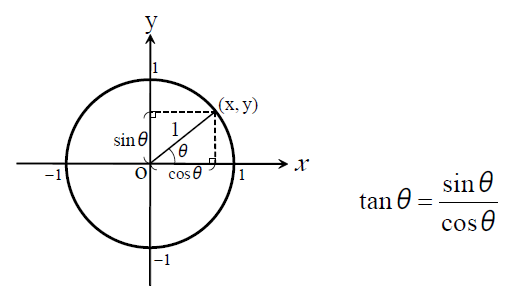
Javaソースコード- tan計算
以下は、Math.sinメソッドとMath.cosメソッドを使ってtanを計算するソースコードです。
0°から90°まで15°おきにtanを計算します。
Tangent.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045
public class Tangent { // tan計算メソッド public static double tan( double deg ) { // 度degをラジアンradに変換 double rad = Math.toRadians( deg ); // cosを計算 double c = Math.cos( rad ); // sinを計算 double s = Math.sin( rad ); // tanを計算 double t = s / c; // tanを戻す return t; } // mainメソッド public static void main( String[] args ) { // 0°のtan System.out.println( tan( 0.0 ) ); // 15°のtan System.out.println( tan( 15.0 ) ); // 30°のtan System.out.println( tan( 30.0 ) ); // 45°のtan System.out.println( tan( 45.0 ) ); // 60°のtan System.out.println( tan( 60.0 ) ); // 75°のtan System.out.println( tan( 75.0 ) ); // 90°のtan System.out.println( tan( 90.0 ) ); } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis Tangent.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac Tangent.java
実行
C:\talavax\javasample>java Tangent
0.0 0.2679491924311227 0.5773502691896256 0.9999999999999999 1.7320508075688767 3.7320508075688776 1.633123935319537E16
出力結果の最後の行はtan90°を計算した結果で「1.633123935319537E16」になりました。
最後の「E16」は数字を指数表記で表したもので10の16乗を表しています。
よって、最後の行の結果は、1.633123935319537×(10の16乗)です。
理論上、tan90°は∞(無限大)になりますが、このプログラムを実行した結果は「1.633123935319537E16」です。
Math.cosメソッドで扱う引数の角度の単位はラジアンです。このソースコードではMath.toRadiansメソッドを使って単位°の角度とラジアンに変換した値を引数としています。
Math.toRadiansメソッド
public static double Math.toRadians( double a )
・引数aで指定した角度をラジアンに変換した値を返します。 パラメータ a : 角度（単位：度）[ 戻り値 ラジアン
Javaソースコード- cos計算
以下は、Math.cosメソッドでcosを計算するソースコードです。
0°から90°まで15°おきにcosを計算します。
Cosine.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039
public class Cosine { // cos計算メソッド public static double cos( double deg ) { // 度degをラジアンradに変換 double rad = Math.toRadians( deg ); // cosを計算 double c = Math.cos( rad ); // cosを戻す return c; } // mainメソッド public static void main( String[] args ) { // 0°のtan System.out.println( cos( 0.0 ) ); // 15°のtan System.out.println( cos( 15.0 ) ); // 30°のtan System.out.println( cos( 30.0 ) ); // 45°のtan System.out.println( cos( 45.0 ) ); // 60°のtan System.out.println( cos( 60.0 ) ); // 75°のtan System.out.println( cos( 75.0 ) ); // 90°のtan System.out.println( cos( 90.0 ) ); } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis Cosine.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac Cosine.java
実行
C:\talavax\javasample>java Cosine
1.0 0.9659258262890683 0.8660254037844387 0.7071067811865476 0.5000000000000001 0.25881904510252074 6.123233995736766E-17
出力結果の最後の行はcos90°を計算した結果で「6.123233995736766E-17」になりました。
最後の「E-17」は数字を指数表記で表したもので10の-17乗を表しています。
よって、最後の行の結果は、6.123233995736766×(10の-17乗)です。
以上です。
関連コンテンツ
広告
