二次方程式の解の公式

2022.10.17

数学

二次方程式、

$二次方程式$

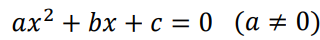
の解を求める式は、

$二次方程式の解の公式$

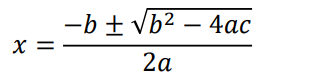
です。これが、二次方程式の解の公式です。

上の式のa≠0は、aが0の場合は、二次方程式の解の公式が使えないことを表しています。公式の分母の2aが0になるので解を導きだせません。

この公式によって導かれる解は、最大２つです。以下のx1とx2です。

平方根の中の式（判別式）が０未満の場合は「解なし」、判別式の計算結果が０の場合は、x1とx2の値が同じになるので解が１つです。

$二次方程式の解の１つ目$

$二次方程式の解の２つ目$

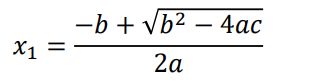
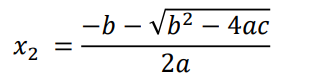
Javaソースコード

以下は、二次方程式のパラメータa、b、cを与えてxを計算するJava ソースコードです。

QuadraticFormula.java

ダウンロード

public class QuadraticFormula {
	// 二次方程式の解
	private static double[] get( double a, double b, double c )
	{
		// 0とみなす値（任意）
		double e = 0.00000000001;

		// aが0でないかを判定
		if ( e > Math.abs( a ) ) return null;	// 解なし

		// 判別式
		double d = b * b - 4.0 * a * c;

		// 判別式で解の存在を判定
		if ( 0.0 > d ) return null;	// 解なし

		// 解を格納する配列
		double[] x = null;
	
		// 解が１つだけ存在
		if ( e > d ) {
			x = new double[ 1 ];
			x[ 0 ] = -b / ( 2.0 * a );
		}
		else {
			// 解が２つ存在
			x = new double[ 2 ];
			x[ 0 ] = ( -b + Math.sqrt( d ) ) / ( 2.0 * a );
			x[ 1 ] = ( -b - Math.sqrt( d ) ) / ( 2.0 * a );
		}

		return x;
	}


	// 結果出力
	private static void output( double[] x, double a, double b, double c )
	{
		// パラメーターの出力
		System.out.println( "a=" + a + ", b=" + b + ", c=" + c );

		// 解がない場合
		if ( null == x ) {
			System.out.println( "解なし" );
			return;
		}

		// 解が１つの場合
		if ( 1 == x.length ) {
			System.out.println( "x=" + x[ 0 ] );
			return;
		}

		// 解が２つの場合
		if ( 2 == x.length ) {
			System.out.println( "x=" + x[ 0 ] + " と x=" + x[ 1 ] );
		}
	} 


	// メイン
	public static void main( String[] args ) {
		// 方程式のパラメータ
		double a, b, c;

		// 解を格納する配列
		double[] x;

		// 3x＾2 - 30x - 48 = 0
		a = 3.0;
		b = -30.0;
		c = 48.0;
		x = get( a, b, c );	// 解の計算
		output( x, a, b, c );	// a,b,cと解を出力

		// 次の出力結果との隙間
		System.out.println();	// 改行

		// x＾2 - 6x + 9 = 0
		a = 1.0;
		b = -6.0;
		c = 9.0;
		x = get( a, b, c );	// 解の計算
		output( x, a, b, c );	// a,b,cと解を出力

		// 次の出力結果との隙間
		System.out.println();	// 改行

		// x＾2 + x + 1 = 0
		a = 1.0;
		b = 1.0;
		c = 1.0;
		x = get( a, b, c );	// 解の計算
		output( x, a, b, c );	// a,b,cと解を出力

		// 次の出力結果との隙間
		System.out.println();	// 改行

		// x - 5 = 0
		a = 0.0;
		b = 1.0;
		c = -5.0;
		x = get( a, b, c );	// 解の計算
		output( x, a, b, c );	// a,b,cと解を出力
	}
}

出力結果

a=3.0, b=-30.0, c=48.0
x=8.0 と x=2.0

a=1.0, b=-6.0, c=9.0
x=3.0

a=1.0, b=1.0, c=1.0
解なし

a=0.0, b=1.0, c=-5.0
解なし

Javaソースコードの解説

public class QuadraticFormula {

クラス名を、QuadraticFormulaとしています。

002
003
004

	// 二次方程式の解
	private static double[] get( double a, double b, double c )
	{

ここから二次方程式の解を計算するメソッドです。引数にdouble型のa、b、cを渡すと、解をdouble型の配列で戻します。

解が２つの場合は配列の要素数が２、１つの場合は配列の要素数が１、解がない場合はnullを戻します。

005
006

		// 0とみなす値（任意）
		double e = 0.00000000001;

0とみなすためのdouble型の値を変数eに代入しています。この値は任意です。必要な精度に応じて変更してください。

008
009

		// aが0でないかを判定
		if ( e > Math.abs( a ) ) return null;	// 解なし

引数aが０かどうかを判定し、０であればreturn文でnullを戻しています。

判定方法は、aの絶対値が０とみなせる値を格納した変数eより小さい場合に０と判定しています。

Math.absメソッド

public static int Math.abs( int a )
public static long Math.abs( long a )
public static float Math.abs( float a )
public static double Math.abs( double a )
public static int Math.abs( byte a )
public static int Math.abs( short a )

・引数aに指定した数値の絶対値を返します。

  パラメータ a : 絶対値を求めたい数値

  戻り値     aの絶対値を返します。
  戻りの変数型は、基本的に引数と同じ変数型と考えてよいです。

011
012

		// 判別式
		double d = b * b - 4.0 * a * c;

二次方程式の解の公式の平方根の中の式を判別式といいます。その判別式にa、b、cを与えて計算しています。

014
015

		// 判別式で解の存在を判定
		if ( 0.0 > d ) return null;	// 解なし

判別式の計算結果dがマイナスがどうかを判定し、マイナスであれば解がないのでnullを戻します。

マイナスの値の平方根が計算できないからです。

017
018

		// 解を格納する配列
		double[] x = null;

解を格納するdouble型の配列を宣言しています。初期値にnullを代入しています。

		// 解が１つだけ存在
		if ( e > d ) {
			x = new double[ 1 ];
			x[ 0 ] = -b / ( 2.0 * a );
		}

判別式の計算結果dが０とみなせる値を格納した変数eより小さい場合に、判別式を０と判定しています。

この処理に到達している場合、既にdが０以上なので、変数eより小さければdは０と判定できます。

判別式の計算結果dが０の場合、解が１つなので、配列xの要素を１つで作成し、判別式を０にして計算した結果を代入しています。

		else {
			// 解が２つ存在
			x = new double[ 2 ];
			x[ 0 ] = ( -b + Math.sqrt( d ) ) / ( 2.0 * a );
			x[ 1 ] = ( -b - Math.sqrt( d ) ) / ( 2.0 * a );
		}

判別式の計算結果dが０より大きい場合、解が２つなので、配列xの要素を２つで作成し、それぞれの解を配列の１つ目と２つ目に代入しています。

Math.sqrtメソッド

public static double Math.sqrt( double a )

・引数aで指定した数値の平方根を返します。

  パラメータ a : 平方根を求める数値

  戻り値     aの平方根

		return x;

解を格納した配列xを戻して終了です。この時点で、配列の要素数は１または２です。

036
037

	// 結果出力
	private static void output( double[] x, double a, double b, double c )

ここから二次方程式のパラメーターa、b、cと解をコンソール出力するメソッドです。引数に解を格納した配列xとdouble型のa、b、cを渡すと結果をコンソール出力します。

039
040

		// パラメーターの出力
		System.out.println( "a=" + a + ", b=" + b + ", c=" + c );

パラメーターa、b、cを横並びでコンソール出力しています。

		// 解がない場合
		if ( null == x ) {
			System.out.println( "解なし" );
			return;
		}

配列xがnullの場合、解がないので、"解なし"をコンソール出力しています。

		// 解が１つの場合
		if ( 1 == x.length ) {
			System.out.println( "x=" + x[ 0 ] );
			return;
		}

配列xの要素数が１の場合、解が１つなので、x[ 0 ]の値をコンソール出力しています。

配列xの要素数は、x.lengthで取得できます。

		// 解が２つの場合
		if ( 2 == x.length ) {
			System.out.println( "x=" + x[ 0 ] + " と x=" + x[ 1 ] );
		}

配列xの要素数が２の場合、解が２つなので、x[ 0 ]とx[ 1 ]の値を横並びでコンソール出力しています。

このソースコードの実行ではないことですが、配列xの要素数が３以上の場合、パラメーターa、b、cだけが出力されます。

061
062

	// メイン
	public static void main( String[] args ) {

このmainメソッドからプログラムを実行します。

063
064

		// 方程式のパラメータ
		double a, b, c;

方程式のパラメーターa、b、cを格納する変数を宣言しています。

066
067

		// 解を格納する配列
		double[] x;

方程式の公式の解を格納するdouble型の配列xを宣言しています。

		// 3x＾2 - 30x - 48 = 0
		a = 3.0;
		b = -30.0;
		c = 48.0;
		x = get( a, b, c );	// 解の計算
		output( x, a, b, c );	// a,b,cと解を出力

パラメーターa=3.0、b=-30.0、c=48.0を二次方程式の解を計算するgetメソッドに渡して、解xを取得しています。

解xとパラメーターa、b、cを結果出力メソッドoutputに渡して、コンソール出力しています。

076
077

		// 次の出力結果との隙間
		System.out.println();	// 改行

次の出力結果との隙間を開けるために改行しています。

		// x＾2 - 6x + 9 = 0
		a = 1.0;
		b = -6.0;
		c = 9.0;
		x = get( a, b, c );	// 解の計算
		output( x, a, b, c );	// a,b,cと解を出力

		// 次の出力結果との隙間
		System.out.println();	// 改行

		// x＾2 + x + 1 = 0
		a = 1.0;
		b = 1.0;
		c = 1.0;
		x = get( a, b, c );	// 解の計算
		output( x, a, b, c );	// a,b,cと解を出力

		// 次の出力結果との隙間
		System.out.println();	// 改行

		// x - 5 = 0
		a = 0.0;
		b = 1.0;
		c = -5.0;
		x = get( a, b, c );	// 解の計算
		output( x, a, b, c );	// a,b,cと解を出力