2023.02.15
数学グラフ
同じマンハッタン距離の座標をプロット
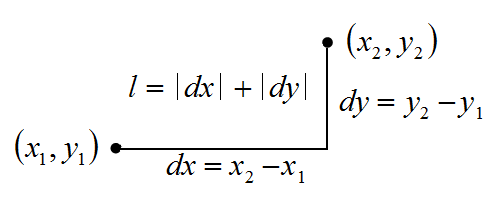
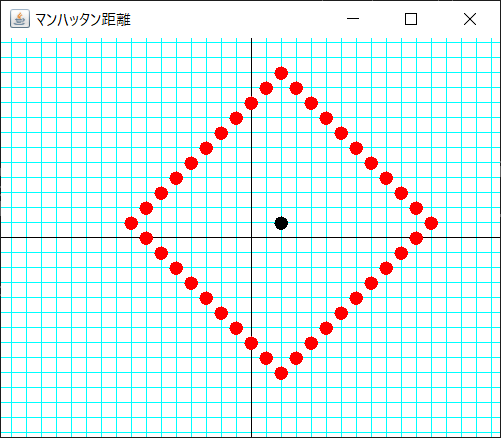
Javaソースコード
Axis2DMHDistance.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071 072 073 074 075 076 077 078 079 080 081 082 083 084 085 086 087 088 089 090 091 092 093 094 095 096 097
import java.awt.*; import javax.swing.*; public class Axis2DMHDistance { public static void main(String[] args) { // フレームの大きさを設定 int w = 400; int h = 320; // フレームを作成 JFrame frame = new JFrame(); // タイトル名を設定 frame.setTitle( "マンハッタン距離" ); // 内側フレームの大きさを設定 frame.getContentPane().setPreferredSize( new Dimension( w, h ) ); frame.pack(); // ”×”ボタンを押した時の処理を設定 frame.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE ); // フレームにパネルを追加 MyPanel panel = new MyPanel(); frame.getContentPane().add( panel ); // フレームを表示 frame.setVisible( true ); } } // JPanelを継承したMyPanelを作成 class MyPanel extends JPanel { public MyPanel() { // 背景色を白(white)に設定 setBackground( Color.white ); } // 描画 public void paintComponent( Graphics g ) { super.paintComponent( g ); // フレームの大きさを取得 int frame_w = getWidth(); int frame_h = getHeight(); // グラフィック座標の原点座標をフレームの真ん中に設定 int ox = frame_w / 2; int oy = frame_h / 2; // グラフィック座標のグリッド幅を設定 int grid_x = 12; int grid_y = 12; // 数学座標のグリッド幅を設定 double scale_x = 1.0; double scale_y = -1.0; // 座標軸とグリッドを描画 // Axis2Dオブジェクトを作成 Axis2D axis = new Axis2D(); // 描画情報を設定 axis.init( frame_w, frame_h, ox, oy, grid_x, grid_y, scale_x, scale_y ); // 描画 axis.draw_grid( g, Color.black, Color.cyan ); // 原点(origin_x,origin_x)から同じマンハッタン距離mdistanceの座標に円を描画 // 原点座標を格納する変数を宣言 int origin_x = 2; int origin_y = 1; // マンハッタン距離を格納する変数を宣言 int mdistance = 10; // 原点座標に 黒の●を描画 axis.draw_fillcircle( g, (double)origin_x, (double)origin_y, 5, Color.black ); // プロット処理 for ( int y = -mdistance; y <= mdistance; y++ ) { for ( int x = -mdistance; x <= mdistance; x++ ) { // 原点(origin_x,origin_x)からのマンハッタン距離mdを計算 int md = Math.abs( x ) + Math.abs( y ); // 計算したマンハッタン距離mdとmdistanceの一致判定 if ( md == mdistance ) { // 赤の●を描画 axis.draw_fillcircle( g, (double)( x + origin_x ), (double)( y + origin_y ), 5, Color.red ); } } } } }
ソースコードの解説
ここから、「Axis2DMHDistance.java」を解説していきます。
001 002
import java.awt.*; import javax.swing.*;
004
public class Axis2DMHDistance {
005
public static void main(String[] args) {
このmainメソッドからプログラムを実行します。
006 007 008
// フレームの大きさを設定 int w = 400; int h = 320;
010 011
// フレームを作成
JFrame frame = new JFrame();
JFrameオブジェクトを作成しています。
013 014
// タイトル名を設定 frame.setTitle( "マンハッタン距離" );
017 018 019
// 内側フレームの大きさを設定
frame.getContentPane().setPreferredSize( new Dimension( w, h ) );
frame.pack();
021 022
// ”×”ボタンを押した時の処理を設定
frame.setDefaultCloseOperation( JFrame.EXIT_ON_CLOSE );
"×"ボタンをクリックしたときに、フレームを閉じる処理を設定しています。
024 025 026
// フレームにパネルを追加
MyPanel panel = new MyPanel();
frame.getContentPane().add( panel );
フレームにパネルに追加しています。
このパネルで、サインカーブのグラフを表示いています。34行目以降を参考にしてください。
028 029
// フレームを表示
frame.setVisible( true );
034 035
// JPanelを継承したMyPanelを作成 class MyPanel extends JPanel {
JPanelを継承したMyPanelクラスを作成しています。
036 037 038
public MyPanel() { // 背景色を白(white)に設定 setBackground( Color.white );
クラス名と同じ名前のメソッドMyPanel()はコンストラクタと呼ばれ、クラス作成時に呼ばれます。そのメソッドの中に初期化の処理を記述します。
ここでは、setBackgroundメソッドにColor.whiteを渡して、背景色を白にする処理を記述しています。
042 043
// 描画 public void paintComponent( Graphics g ) {
044
super.paintComponent( g );
046 047 048
// フレームの大きさを取得 int frame_w = getWidth(); int frame_h = getHeight();
050 051 052
// グラフィック座標の原点座標をフレームの真ん中に設定 int ox = frame_w / 2; int oy = frame_h / 2;
グラフィック座標の原点座標(ox,oy)を設定しています。ここでは、フレームの中心座標が原点になるようにしています。
054 055 056
// グラフィック座標のグリッド幅を設定 int grid_x = 12; int grid_y = 12;
058 059 060
// 数学座標のグリッド幅を設定 double scale_x = 1.0; double scale_y = -1.0;
数学座標のグリッド幅scale_x、グリッド高さscale_yを設定しています。
ここでは、変数scale_xに1.0、変数scale_yに-1.0を代入しています。
これで、X方向の12pixel(grid_x=12)が数学座標で1.0を表し、Y方向の12pixel(grid_y=12)が数学座標で-1.0を表したことになります。
グラフィック座標系のY軸の＋（プラス）は下方向で、XY座標系のY軸の＋（プラス）は上方向です。変数scale_yにマイナス値を代入することで数学座標系のY軸の＋（プラス）が上方向になります。
062
// 座標軸とグリッドを描画
ここから、座標軸とグリッドを描画する処理です。
063 064
// Axis2Dオブジェクトを作成
Axis2D axis = new Axis2D();
Axis2Dのオブジェクトaxisを作成しています。
066 067
// 描画情報を設定
axis.init( frame_w, frame_h, ox, oy, grid_x, grid_y, scale_x, scale_y );
描画する情報を設定しています。
Axis2D.initメソッド
public boolean init( int fw, int fh, int ox, int oy, int gx, int gy, double sx, double sy )
・描画するxy-座標の情報を設定します。
パラメータ fw : フレームの横のピクセル数
fh : フレームの縦のピクセル数
ox : グラフィック座標の原点xの位置(pixel)
oy : グラフィック座標の原点yの位置(pixel)
gx : グラフィック座標のグリッドの幅(pixel)
gy : グラフィック座標のグリッドの高さ(pixel)
sx : 数学座標のグリッドの幅(gxあたりの幅)
例）sx=1.0を指定した場合、数学座標でのグリッド幅は1.0になり、右方向が＋(プラス)となります。
例）sx=-0.5を指定した場合、数学座標でのグリッド高は-0.5になり、右方向が－(マイナス)となります。
sy : 数学座標のグリッドの高さ(gyあたりの高さ)
例）sy=-1.0を指定した場合、数学座標でのグリッド幅は-1.0になり、上方向が＋(プラス)となります。
例）sy=1.0を指定した場合、数学座標でのグリッド高は1.0になり、上方向が－(マイナス)となります。
グラフィック座標のY軸のプラス方向は下で、数学座標のY軸のプラス方向は上です。
このメソッドでは、syにマイナスを代入することで数学座標の上方向をプラスにしています。
戻り値 true : 設定に成功
false : 設定に失敗
069 070
// 描画
axis.draw_grid( g, Color.black, Color.cyan );
ここで描画しています。座標軸の色は黒（Color.black）、グリッド線の色はシアン（Color.cyan）にしています。
Axis2D.draw_gridメソッド
public void draw_grid( Graphics g, Color axiscolor, Color gridcolor )
・座標軸とグリッドを描画します。 パラメータ g : 描画するGraphicsオブジェクト axiscolor : 座標軸の色 gridcolor : グリッド(格子)の色 戻り値 なし 詳細 initメソッドで設定後に、このメソッドを呼ぶとGraphicsオブジェクトに座標とグリッドを描画します。座標軸とグリッドの線幅は1です。
072 073 074 075
// 原点(origin_x,origin_x)から同じマンハッタン距離mdistanceの座標に円を描画 // 原点座標を格納する変数を宣言 int origin_x = 2; int origin_y = 1;
マンハッタン距離を計算する基準の座標を格納するint型の変数を宣言し、初期値を代入しています。
origin_xは基準のx座標、origin_yは基準のy座標です。
ここでは座標( 2, 1 )を指定していますが、任意の値に変更してもよいです。
077 078
// マンハッタン距離を格納する変数を宣言 int mdistance = 10;
080 081
// 原点座標に 黒の●を描画 axis.draw_fillcircle( g, (double)origin_x, (double)origin_y, 5, Color.black );
Axis2D.draw_fillcircleメソッド
public void draw_fillcircle( Graphics g, double x, double y, int radius, Color color )
・塗りつぶし円を描画します。 パラメータ g : 描画するGraphicsオブジェクト x : 数学座標の円の中心座標x y : 数学座標の円の中心座標y radius : グラフィック座標の円の半径 color : 色 戻り値 なし 詳細 initメソッドで設定後に、このメソッドを呼んでください。
083 084 085
// プロット処理 for ( int y = -mdistance; y <= mdistance; y++ ) { for ( int x = -mdistance; x <= mdistance; x++ ) {
基準座標( origin_x, origin_y )との距離がmdistanceになる座標の範囲は、
( origin_x - mdistance, origin_y - mdistance ) - ( origin_x + mdistance, origin_y + mdistance )
です。
086 087
// 原点(origin_x,origin_x)からのマンハッタン距離mdを計算 int md = Math.abs( x ) + Math.abs( y );
int md = Math.abs( ( origin_x + x ) - origin_x ) + Math.abs( ( origin_y + y ) - origin_y );
となりますが、上記のコードからorigin_xとorigin_yは引き算によって0になるので、
int md = Math.abs( x ) + Math.abs( y );
としています。
089 090 091 092 093
// 計算したマンハッタン距離mdとmdistanceの一致判定 if ( md == mdistance ) { // 赤の●を描画 axis.draw_fillcircle( g, (double)( x + origin_x ), (double)( y + origin_y ), 5, Color.red ); }
計算によって求めたマンハッタン距離mdと指定したマンハッタン距離mdistanceが同じ場合、座標( origin_x + x, origin_y + y )に赤色の●を描画しています。円の半径は5にしています。
色と半径は、変更してもよいです。
以上です。
Axis2DMHDistanceのコンパイル
コンパイルには、"Axis2DMHDistance.java"の他に、「Axis2D.java」と「Transformation2d.java」が必要です。
以下の記事から取得してください。
コンパイル方法
javac Axis2DMHDistance.java
コンパイル方法（ソースの文字コードが"ANSI"の場合）
javac -encoding sjis Axis2DMHDistance.java
コンパイル方法（ソースの文字コードが"utf-8"の場合）
javac -encoding utf-8 Axis2DMHDistance.java
次に読んでほしいコンテンツ
関連コンテンツ
広告
