2020.03.23
数学
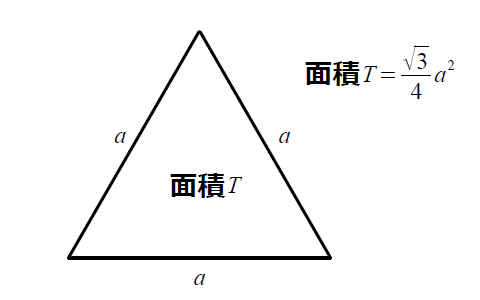
正三角形の面積計算
1辺の長さaの正三角形の面積を求める公式があります。その計算式は以下の通りです。
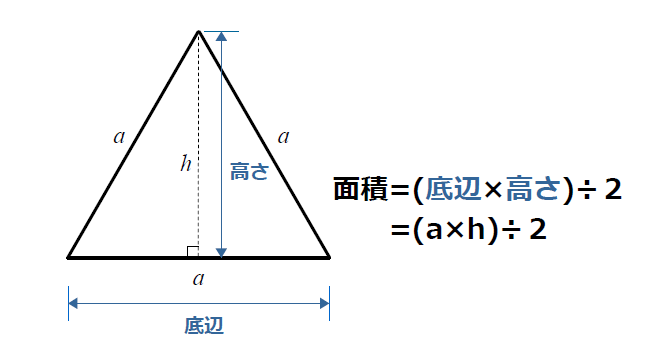
それでは、高さhを計算で求める方法を説明します。
1つめの方法は、ピタゴラスの定理を使って高さh求める方法です。
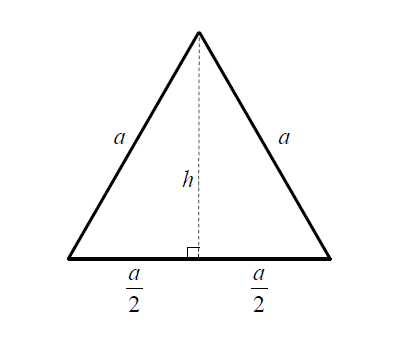
斜辺の長さはaで、その他の辺の長さはhと(a/2)です。これをピタゴラスの定理に当てはめると
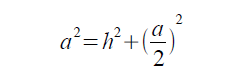
となります。
これを高さhが左辺になるように式に変形すると
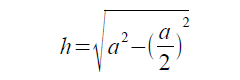
となります。
右辺を計算して式を簡単にしていくと、以下の結果は得られます。
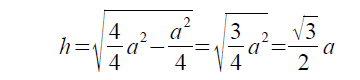
これが、正三角形の1辺の長さと高さの関係式です。
ここで求めた高さhを使って三角形の面積Tを求めると
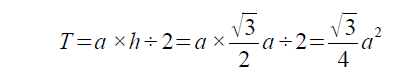
という式が得られます。この式は、冒頭に記載している面積計算の公式と一致しています。
次に、2つ目の方法を説明します。この方法は三角関数を使って高さhを求める方法です。
正三角形の内角は60°であり、斜辺の長さがaなので、三角形のsinθを利用することで高さを求めることができます。sin60°は√3/2なので、高さh=a×sin60°で計算することができます。
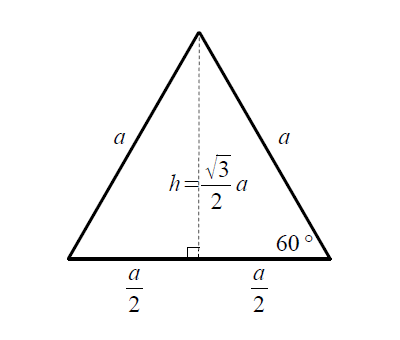
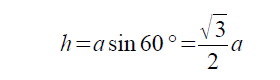
ここで求めた高さhは、ピタゴラスの定理を使って求めたhと同じになりました。
以上です。
正三角形の面積計算に関するコンテンツ
「正三角形の面積計算」に関係があるコンテンツをまとめています。


