2025.06.12
直線と点の距離
はじめに
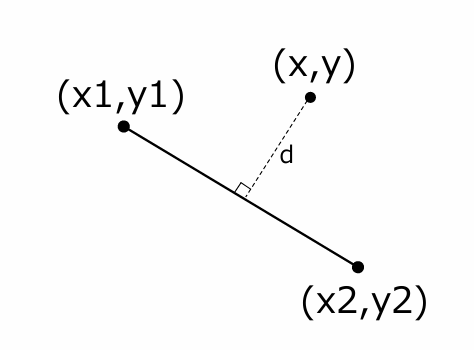
直線と点の距離は、点から直線におろした垂線の長さです。
ここでは、直線と点の距離を求める一般的な公式を使わずに、(x1,y1)と(x2,y2)と(x,y)を頂点とする三角形の面積を利用して距離を計算する方法を使います。
直線と点の距離の計算方法
辺aの長さ : (x1,y1)と(x2,y2)の直線距離 辺bの長さ : (x1,y1)と(x,y)の直線距離 辺cの長さ : (x2,y2)と(x,y)の直線距離
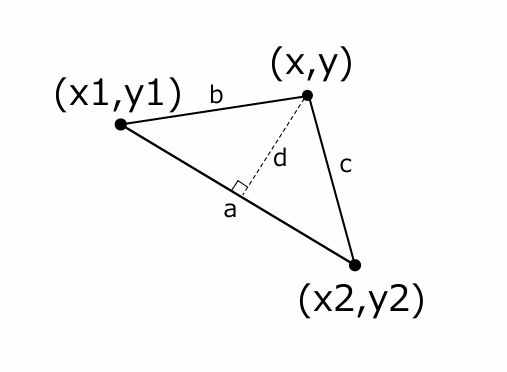
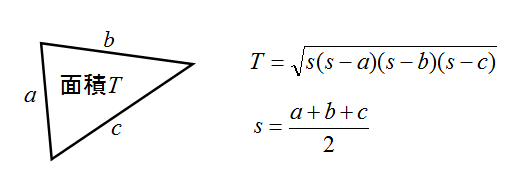
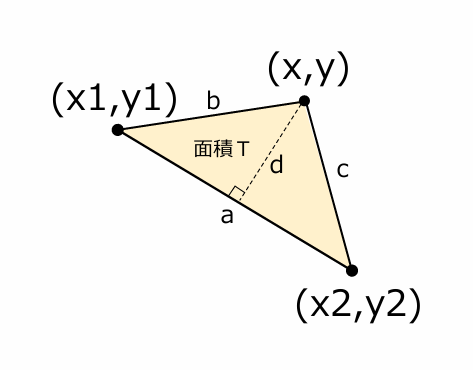
三角形の面積T = a × d ÷ 2
これをdを計算する式にすると、
d = 三角形の面積T ÷ a × 2
となります。
この方法で、直線と点の距離を求めることができます。
Javaソースコード
以下は、ヘロンの公式を使って直線と点の距離を求めるJavaソースコードです。
DistanceHeron.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071 072 073 074 075 076 077 078 079 080 081 082 083 084 085 086 087 088 089 090 091 092 093 094 095 096 097 098 099 100 101 102 103 104
public class DistanceHeron { // 3角形の3辺の長さa,b,cから面積を計算するメソッド private static double herons_formula( double a, double b, double c ) { double s; // s = ( a + b + c ) / 2 double t; // 面積 double d; // 作業用変数 // 3辺のどれか1つでも0より小さければ-1.0を返す if ( ( 0.0 > a ) || ( 0.0 > b ) || ( 0.0 > c ) ) return -1.0; // sを計算 s = ( a + b + c ) / 2.0; // s(s-a)(s-b)(s-c)を計算し、マイナスになれば-1.0を返す d = s * ( s - a ) * ( s - b ) * ( s - c ); if ( 0.0 > d ) return -1.0; // 面積tを計算 t = Math.sqrt( d ); // 計算した面積tを返す return t; } // (x1,y1)-(x2,y2)の直線距離を計算するメソッド private static double dist( double x1, double y1, double x2, double y2 ) { double l; double dx, dy; // x座標の差を計算してdxに代入 dx = x2 - x1; // y座標の差を計算してdyに代入 dy = y2 - y1; // 2点間の距離を計算してlに代入 l = Math.sqrt( dx * dx + dy * dy ); // 計算した距離を返す return l; } // (x1,y1)-(x2,y2)を通る直線と点(x,y)の直離を計算するメソッド private static double dist_ltop( double x1, double y1, double x2, double y2, double x, double y ) { double a, b, c; // 3辺の長さ double t; // 3角形の面積 double d; // 求める距離 double eps = 0.0000000000000000000000001; // 0と判定する値(任意の値) // 3角形の各辺の長さを計算 a = dist( x1, y1, x2, y2 ); b = dist( x, y, x1, y1 ); c = dist( x, y, x2, y2 ); // 3角形の面積を計算 t = herons_formula( a, b, c ); if ( 0.0 > t ) return -1.0; // 直線と点の距離を計算 if ( eps < a ) d = t * 2.0 / a; // 直線と点の距離を計算結果をdに代入 else d = b; // (x1,y1)と(x,y)の直線距離をdに代入 return d; } // メイン public static void main( String[] args ) { // 変数の宣言 double x1, y1; // 直線の1点目の座標 double x2, y2; // 直線の2点目の座標 double x, y; // 点の座標 double d; // 求める距離 // 直線の1つめの座標(x1,y1)を代入 x1 = 0.0; y1 = 10.0; // 直線の2つめの座標(x2,y2)を代入 x2 = 10.0; y2 = 0.0; // 点の座標(x,y)を代入 x = 10.0; y = 10.0; // 直線と点の距離を計算 d = dist_ltop( x1, y1, x2, y2, x, y ); if ( 0.0 > d ) { System.out.println( "3角形の面積計算に失敗しました" ); return; } // 結果を出力 System.out.println( d ); } }
実行結果
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis DistanceHeron.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac DistanceHeron.java
DistanceHeronを実行
C:\talavax\javasample>java DistanceHeron
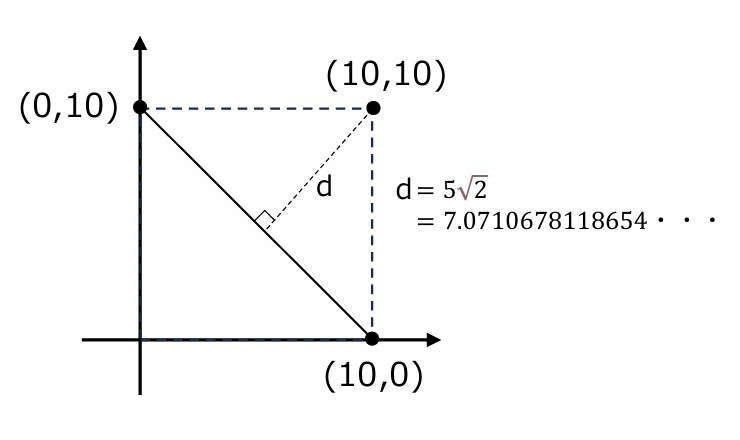
7.071067811865475
√(102+102) = √200 = 10√2
です。この値の半分の「5√2」が距離になります。
Javaソースコードの解説
ここからは、このソースコードを上から順番に解説していきます。
001
public class DistanceHeron {
クラス名を、DistanceHeronとしています。
002 003 004
// 3角形の3辺の長さa,b,cから面積を計算するメソッド private static double herons_formula( double a, double b, double c ) {
005 006 007
double s; // s = ( a + b + c ) / 2 double t; // 面積 double d; // 作業用変数
009 010
// 3辺のどれか1つでも0より小さければ-1.0を返す
if ( ( 0.0 > a ) || ( 0.0 > b ) || ( 0.0 > c ) ) return -1.0;
与えられた3つの引数のうち1つでも0.0より小さい場合は、エラーとして-1.0を返しています。
012 013
// sを計算
s = ( a + b + c ) / 2.0;
ヘロンの公式で使うsを計算しています。
015 016 017
// s(s-a)(s-b)(s-c)を計算し、マイナスになれば-1.0を返す
d = s * ( s - a ) * ( s - b ) * ( s - c );
if ( 0.0 > d ) return -1.0;
s,a,b,cをヘロンの公式の平方根に渡す値dを計算しています。これは、平方根を計算するMath.sqrtメソッドにマイナスの値を渡さないようするためです。値がマイナスであれば-1.0を返すようにしています。
019 020
// 面積tを計算
t = Math.sqrt( d );
Math.sqrtメソッド
public static double Math.sqrt( double a )
・引数aで指定した数値の平方根を返します。 パラメータ a : 平方根を求める数値 戻り値 aの平方根
022 023
// 計算した面積tを返す return t;
027 028 029
// (x1,y1)-(x2,y2)の直線距離を計算するメソッド private static double dist( double x1, double y1, double x2, double y2 ) {
030 031
double l; double dx, dy;
033 034
// x座標の差を計算してdxに代入
dx = x2 - x1;
035 036
// y座標の差を計算してdyに代入
dy = y2 - y1;
038 039
// 2点間の距離を計算してlに代入
l = Math.sqrt( dx * dx + dy * dy );
下の図は、2つの座標間の距離を計算する方法を示した図で、lが2点間の距離で、dxがX方向の差を、dyがY方向の差を表しています。これをピタゴラスの定理に当てはめると、lが斜辺、dxとdyがその他の2辺です。2点の座標の位置関係によって、2つの辺の長さ(dxとdy)がマイナス(-)の値になることがありますが、これらの値は計算時に2乗するので、結果的に符号が無視され、正しい結果が得られます。
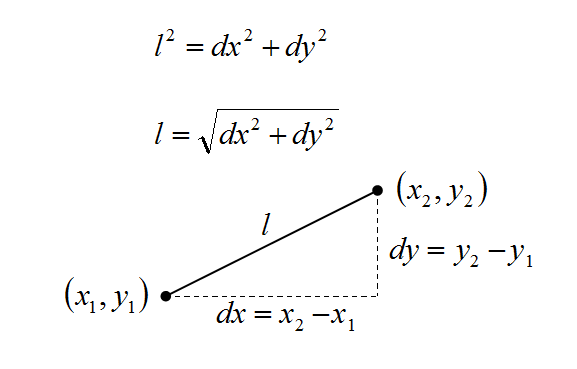
041 042
// 計算した距離を返す return l;
046 047 048
// (x1,y1)-(x2,y2)を通る直線と点(x,y)の直離を計算するメソッド private static double dist_ltop( double x1, double y1, double x2, double y2, double x, double y ) {
049 050 051 052
double a, b, c; // 3辺の長さ double t; // 3角形の面積 double d; // 求める距離 double eps = 0.0000000000000000000000001; // 0と判定する値(任意の値)
054 055 056 057
// 3角形の各辺の長さを計算
a = dist( x1, y1, x2, y2 );
b = dist( x, y, x1, y1 );
c = dist( x, y, x2, y2 );
059 060
// 3角形の面積を計算
t = herons_formula( a, b, c );
061
if ( 0.0 > t ) return -1.0;
063 064 065 066 067
// 直線と点の距離を計算 if ( eps < a ) d = t * 2.0 / a; // 直線と点の距離を計算結果をdに代入 else d = b; // (x1,y1)と(x,y)の直線距離をdに代入
距離d = 三角形の面積T ÷ a × 2
辺aの長さが0.0の場合は辺bの長さを距離dに代入しています。
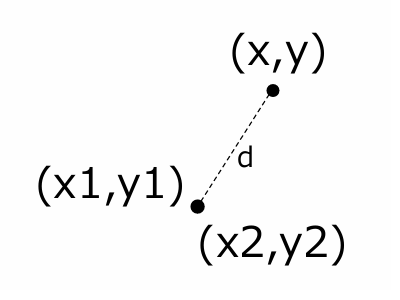
辺aの長さが0.0であるかの判定は、変数aが変数epsの値より大きいという条件を使っています。
あらかじめ変数epsに0.0と判定できる値を代入しています。これは、距離dの長さを計算する際に0.0で割り算をすることを防ぐためです。
epsの値は任意ですが、割り算でエラーにならない値に設定する必要があります。
073 074 075
// メイン public static void main( String[] args ) {
076 077 078 079 080
// 変数の宣言 double x1, y1; // 直線の1点目の座標 double x2, y2; // 直線の2点目の座標 double x, y; // 点の座標 double d; // 求める距離
082 083 084 085 086 087 088
// 直線の1つめの座標(x1,y1)を代入 x1 = 0.0; y1 = 10.0; // 直線の2つめの座標(x2,y2)を代入 x2 = 10.0; y2 = 0.0;
090 091 092
// 点の座標(x,y)を代入
x = 10.0;
y = 10.0;
点の座標(x,y)の値を代入しています。
ここでは、(10,10)を代入しています。
094 095
// 直線と点の距離を計算
d = dist_ltop( x1, y1, x2, y2, x, y );
096 097 098 099
if ( 0.0 > d ) {
System.out.println( "3角形の面積計算に失敗しました" );
return;
}
距離dが0.0未満の場合は計算に失敗しているので、printlnメソッドでエラーメッセージをコンソール出力して、returnによってmainメソッドを抜けています。
101 102
// 結果を出力
System.out.println( d );
printlnメソッドで距離dを出力しています。
以上です。


