2022.09.27

Javaプログラミング

円周上のランダムな座標を求める1

円周上のランダムな座標を求める その１

原点(0,0)、半径rで表す円の上の座標を乱数を使って求めるソースコードを紹介しています。

下の図のように、角度θと半径rを与えることで座標(x,y)を計算することができます。

ここで紹介するソースコードでは、固定した半径rの値と、角度θを乱数で発生させた値からランダムな円周上の座標を計算しています。

角度θと半径rと(x,y)の関係
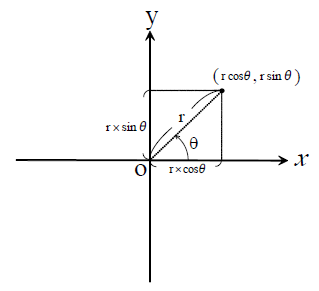
角度θと半径rから(x,y)を求める

Javaソースコード

PointOnCircle1.java

001
002
003
004
005
006
007
008
009
010
011
012
013
014
015
016
017

public class PointOnCircle1 {
	public static void main( String[] args ) {
		// 半径を指定
		double radius = 100.0;

		// 乱数でラジアンを求める
		double rad = 2.0 * Math.PI * Math.random();

		// 原点(0,0)、半径radiusの円周上の(x,y)を計算
		double x = radius * Math.cos( rad );
		double y = radius * Math.sin( rad );
		
		// 結果を出力
		System.out.println( "x=" + x );
		System.out.println( "y=" + y );
	}
}

コンパイル ソースコードが「ANSI」の場合

C:\talavax\javasample>javac -encoding sjis PointOnCircle1.java

コンパイル ソースコードが「UTF-8」の場合

C:\talavax\javasample>javac PointOnCircle1.java

実行

C:\talavax\javasample>java PointOnCircle1

出力結果(実行する毎に結果が変わります)

x=-98.09905147271276
y=19.40556879233515

Javaソースコードの解説

001

public class PointOnCircle1 {

クラス名を、PointOnCircle1としています。

002

	public static void main( String[] args ) {

このmainメソッドからプログラムを実行します。

003
004

		// 半径を指定
		double radius = 100.0;

半径を格納する変数radiusに100.0を代入しています。この値を色々変えてみてください。

006
007

		// 乱数でラジアンを求める
		double rad = 2.0 * Math.PI * Math.random();

ラジアンを格納する変数radに、0.0～2πの範囲で発生する乱数を代入しています。

Math.PIは定数でπ(パイ)の値3.141592…です。

次に呼び出すMath.cosメソッドとMath.sinメソッドは、ラジアンの角度が引数なので、0.0～2πの乱数を発生しています。

009
010
011

		// 原点(0,0)、半径radiusの円周上の(x,y)を計算
		double x = radius * Math.cos( rad );
		double y = radius * Math.sin( rad );

半径radiusに、Math.cos( rad )を掛けてx座標の値を計算しています。同様にMath.sin( rad )を掛けてy座標の値を計算しています。

013
014
015

		// 結果を出力
		System.out.println( "x=" + x );
		System.out.println( "y=" + y );

求めた座標(x,y)をprintlnメソッドでコンソール出力しています。

以上です。

円周上の座標に関するコンテンツ

「円周上の座標」に関係があるコンテンツをまとめています。

プロになるJava?仕事で必要なプログラミングの知識がゼロから身につく最高の指南書

スッキリわかるJava入門 第3版 スッキリわかるシリーズ

スッキリわかるJava入門 実践編 第3版 スッキリわかるシリーズ

前 □ 次(円周上のランダムな座標を求める その２)

次に読んでほしいコンテンツ

Javaの学習に役立つソースコードを多数紹介しています。是非、ご覧ください。

2022.09.10

平面上の位置を表す座標系の１つである「極座標系」について詳しく解説。

2024.11.27

平面上の位置を表す座標系の１つXY座標系について詳しく解説。

2020.03.23

sin（サイン）の意味と、Math.sinメソッドの使い方をソースコードを使って詳しく解説しています。

2020.03.23

cos（コサイン）の意味と、Math.cosメソッドの使い方をソースコードを使って詳しく解説しています。

2020.03.23

円の中心座標(0,0)、半径rで表される円の円周上のランダムな座標を求めるJavaのソースコードを紹介しています。度単位の角度の乱数をラジアンに変換して座標を計算しています。

2019.09.27

円の中心座標(ox,oy)、半径rで表される円の円周上のランダムな座標を求めるJavaのソースコードを紹介しています。

2019.09.27

Javaを使った簡単な応用プログラム（生年月日から年齢を計算プログラムなど）を紹介しています。

2022.07.07

変数やクラスに格納されている値をコンソール出力する方法は？

2020.03.23

プログラムの最初に実行されるメソッドは？

2022.12.13

プログラミングで使う変数って何？

2020.03.23

Javaのプログラムを書いてみませんか？プログラムの書き方をくわしく説明しています。

2020.03.23

「Javaソースコード」から実行可能な「オブジェクトコード」に変換する方法をくわしく説明しています。

2020.03.23

Javaのプログラムを作ってみませんか？プログラミングに必要なものの用意から実行までを説明しています。

2020.03.23

Swingパッケージを使ってグラフィック表示を行う方法を解説しています。

2020.03.23

画像フォーマット形式・色・大きさ・傾きなどの変更、特定の図形（文字・記号など）を見つけたり、取り出したりする画像処理について詳しく解説。

2015.11.29

繰り返し処理を使ったJavaのソースコードサンプルを紹介しています。

2020.03.23

配列を使うJavaソースコードを多数紹介しています。

2021.05.18

数学に関係するJavaのメソッドやソースコードなどを紹介しています。

2022.10.25

三角形、台形、円などいろいろな図形の面積を計算するプログラムを紹介しています。詳しくは、記事をご覧ください。

2021.05.18

StringクラスとStringBuilderクラスを利用したプログラミングの仕方を紹介しています。

2016.12.16

プログラミング、ＩＴに関する用語をまとめています。

2022.10.17

日本で使われてきた伝統文様「和柄」について解説しています。

2022.07.27

関連コンテンツ

乱数の意味と、Math.randomメソッドの使い方をソースコードを使って詳しく解説しています。

2015.12.27

Javaのプログラムを書いてみませんか？プログラムの書き方をくわしく説明しています。

2020.03.23

円の直径と半径について図を使って詳しく解説しています。

2020.03.23

平面上の位置を表す座標系の１つXY座標系について詳しく解説。

2020.03.23

国際単位系における角度の単位のラジアンについて説明しています。興味のある方は、記事をご覧ください。

2016.01.26

円周率、πってどうゆう意味？

2020.03.23

Javaプログラムの構成について解説しています。詳しくは、こちらをご覧ください。

2020.03.23

プログラムの最初に実行されるメソッドは？

2022.12.13

プログラミングで使う変数って何？

2020.03.23

予約語？、定数？

2020.03.23

cos（コサイン）の意味と、Math.cosメソッドの使い方をソースコードを使って詳しく解説しています。

2020.03.23

sin（サイン）の意味と、Math.sinメソッドの使い方をソースコードを使って詳しく解説しています。

2020.03.23

メソッドの定義方法を詳しく解説しています。Javaのサンプルソースコードを使った説明もあります。

2020.03.23

変数やクラスに格納されている値をコンソール出力する方法は？

2020.03.23

「ゆるゆるプログラム」のコンテンツを紹介しています。興味のある方はこの記事をご覧ください。

2020.03.23

Javaの学習に役立つソースコードを多数紹介しています。是非、ご覧ください。

2022.09.10

Javaを使った簡単な応用プログラム（生年月日から年齢を計算プログラムなど）を紹介しています。

2022.07.07

Swingパッケージを使ってグラフィック表示を行う方法を解説しています。

2020.03.23

画像フォーマット形式・色・大きさ・傾きなどの変更、特定の図形（文字・記号など）を見つけたり、取り出したりする画像処理について詳しく解説。

2015.11.29

三角形、台形、円などいろいろな図形の面積を計算するプログラムを紹介しています。詳しくは、記事をご覧ください。

2021.05.18

配列を使うJavaソースコードを多数紹介しています。

2021.05.18

繰り返し処理を使ったJavaのソースコードサンプルを紹介しています。

2020.03.23

数学に関係するJavaのメソッドやソースコードなどを紹介しています。

2022.10.25

StringクラスとStringBuilderクラスを利用したプログラミングの仕方を紹介しています。

2016.12.16

日本で使われてきた伝統文様「和柄」について解説しています。

2022.07.27

プログラミング、ＩＴに関する用語をまとめています。

2022.10.17

広告

【PR】初心者も安心のサポート充実【DMM FX】