三角関数計算方法

2017.08.09

はじめに

Math.sin／Math.cos／Math.tanを使わずに、指定角度の三角関数の値を(sin,cos,tan)を計算するアルゴリズムを紹介します。

ここで紹介するアルゴリズムは、指定された角度の単位ベクトル(x,y)を求め、xをcos、yをsin、y/xをtanとするものです。指定角度の単位ベクトルの求め方は、以下のとおりです。

計算方法

①計算するために与えられた角度が、どの象限に入っているか、また、座標軸上にあるかを判定します。

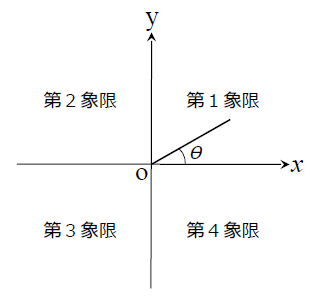
下の図は、象限を表しているもので、角度 θ、0°<θ<90°であれば第1象限、90°<θ<180°であれば第2象限、180°<θ<270°であれば第3象限、270°<θ<360°であれば第4象限に入ることを表しています。角度が0°／90°／180°／270°の場合は、座標軸上です。

②その象限をに対応する座標軸の単位ベクトルを２つ決めます。

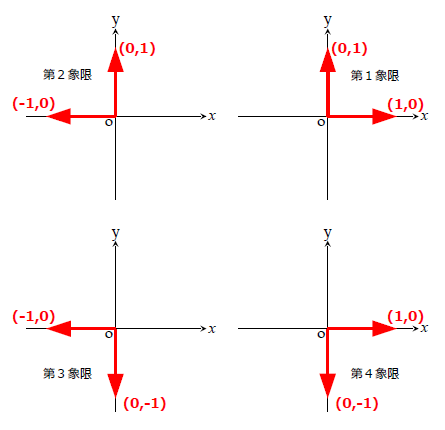
その対応する２つの単位ベクトルを赤矢印で示します。（下図）

下図は、指定角度60°のときに選択された２つの単位ベクトルです。

$各象限に対応する単位ベクトル$

③２つの単位ベクトルの先部分の座標の中点（２つの座標の平均）を通り、原点(0,0)を始点とする単位べクトルを求めます。

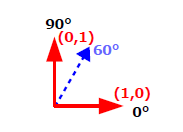
同時に、求めた単位ベクトルのＸ軸からの角度も計算します。これも計算に使用した２つの単位ベクトルの角度の平均で求められます。計算した角度が指定角度に近ければ、この単位ベクトルが求める結果でとなり、処理を終了します。

下図は、0°と90°の間の単位ベクトルを求めています。角度は(0°+90°)/2=45°です。

$各象限に対応する単位ベクトル$

④２つの単位ベクトルのうち１つを③で求めた単位ベクトルに変えます。単位ベクトルの選択条件は、変更後の単位ベクトル角度の範囲内に、指定角度が入ることです。

下図は、0°の単位ベクトルを45°の単位ベクトルに変更した例です。60°の単位ベクトルが２つの単位ベクトルに挟まれていることが分かります。

$各象限に対応する単位ベクトル$

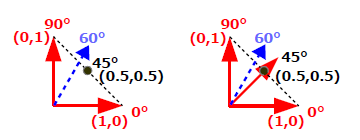
⑤変更後の単位ベクトルで③の処理に戻ります。

このように単位ベクトルの間の角度を1/2ずつ狭めていき、指定の角度まで近づけます。

Javaソースコード

このアルゴリズムをJavaのプログラムにしたものが以下です。

このプログラムで指定する角度の単位は度（°）で、0～359.9999..の範囲を超えて指定した場合でも、自動でこの範囲内に収める処理も含めています。

TriFunction.java

ダウンロード

public class TriFunction {
	// 角度から象限を求める
	static int GetOrthant( double deg )
	{
		if ( (   0.0 < deg ) && (  90.0 > deg ) ) return 1;
		if ( (  90.0 < deg ) && ( 180.0 > deg ) ) return 2;
		if ( ( 180.0 < deg ) && ( 270.0 > deg ) ) return 3;
		if ( ( 270.0 < deg ) && ( 360.0 > deg ) ) return 4;
		return 0;
	}


	public static void main(String[] args) {
		int    orthant;		// 角度を含む象限
		int    loopnumber;	// ループ回数
		double delta;		// 処理終了条件(角度の差)
		// 計算に使用
		double deg, rad;
		double deg1, deg2, degm;
		double x1, y1;
		double x2, y2;
		double mx, my, d;
		double new_x, new_y;
		// 計算結果(sin,cos,tan)
		double ans_sin, ans_cos, ans_tan;

		// 入力した引数が１以上かを調べる
		if ( 1 > args.length ) {
			// 入力した引数が１未満の場合、使用方法を表示する
			System.out.println( 
				"TriFunction [角度(°)]" );
			return;
		}

		// １番目の引数の値をdegに代入
		try {
			// 引数を変換し、角度degに代入
			deg = Double.valueOf( args[ 0 ] );
		}
		catch( NumberFormatException ne )
		{
			System.out.println( "引数が不正です" );
			return;
		}

		// 角度degを0.0～359.999...の範囲に直す
		for ( ; ; ) {
			// degが0.0未満
			if ( 0.0 > deg ) {
				deg += 360.0;
				continue;
			}
			// degが360.0以上
			if ( 360.0 <= deg ) {
				deg -= 360.0;
				continue;
			}
			// ループを抜ける
			break;
		}

		// 結果の初期化
		ans_sin = ans_cos = ans_tan = 0.0;
		loopnumber = 0;

		// 角度から象限を求める
		orthant = GetOrthant( deg );
		x1 = y1 = x2 = y2 = 0.0;
		deg1 = deg2 = 0.0;
		switch ( orthant )
		{
			case 1:
				deg1 = 0.0;
				deg2 = 90.0;
				x1 =  1.0;
				y1 =  0.0;
				x2 =  0.0;
				y2 =  1.0;
				break;

			case 2:
				deg1 = 90.0;
				deg2 = 180.0;
				x1 =  0.0;
				y1 =  1.0;
				x2 = -1.0;
				y2 =  0.0;
				break;

			case 3:
				deg1 = 180.0;
				deg2 = 270.0;
				x1 = -1.0;
				y1 =  0.0;
				x2 =  0.0;
				y2 = -1.0;
				break;

			case 4:
				deg1 = 270.0;
				deg2 = 360.0;
				x1 =  0.0;
				y1 = -1.0;
				x2 =  1.0;
				y2 =  0.0;
				break;

			default:
				// 0°
				if ( 0.0 == deg ) {
					ans_sin = 0.0;
					ans_cos = 1.0;
					ans_tan = ans_sin / ans_cos;
					break;
				}
				// 90°
				if ( 90.0 == deg ) {
					ans_sin = 1.0;
					ans_cos = 0.0;
					ans_tan = ans_sin / ans_cos;
					break;
				}
				// 180°
				if ( 180.0 == deg ) {
					ans_sin = 0.0;
					ans_cos = -1.0;
					ans_tan = ans_sin / ans_cos;
					break;
				}
				// 270°
				if ( 270.0 == deg ) {
					ans_sin = -1.0;
					ans_cos = 0.0;
					ans_tan = ans_sin / ans_cos;
					break;
				}

				// 原因不明のエラー
				System.out.println( "原因不明のエラー" );
				return;
		}

		// 角度が0/90/180/270以外
		if ( 1 <= orthant ) {
			delta = 0.000000001;
			// 無限ループ
			for ( ; ; ) {
				// ループ回数
				++ loopnumber;

				// 角度の中間値を計算
				degm = ( deg1 + deg2 ) / 2.0;

				// 座標の中間点を計算
				mx = ( x1 + x2 ) / 2.0;
				my = ( y1 + y2 ) / 2.0;

				// 原点(0,0)と(mx,my)を結ぶ線の
				// 単位ベクトル(new_x, new_y)を計算
				d = Math.sqrt( mx * mx + my * my );
				new_x = mx / d;
				new_y = my / d;

				// 角度の差がdelta未満で終了
				if ( Math.abs( degm - deg ) < delta ) {
					ans_sin = new_y;
					ans_cos = new_x;
					ans_tan = ans_sin / ans_cos;
					break;
				}

				// 角度を狭める
				if ( deg > degm ) {
					x1 = new_x;
					y1 = new_y;
					deg1 = degm;
				}
				else {
					x2 = new_x;
					y2 = new_y;
					deg2 = degm;
				}
			}
		}

		// 結果の表示
		System.out.println( "■計算結果" );
		System.out.println( "sin(" + deg + ")=" + ans_sin );
		System.out.println( "cos(" + deg + ")=" + ans_cos );
		System.out.println( "tan(" + deg + ")=" + ans_tan );
		System.out.println( "ループ回数=" + loopnumber );

		System.out.println();

		System.out.println( "■Mathクラスでの計算結果" );
		rad = Math.toRadians( deg );
		System.out.println( "sin(" + deg + ")=" + Math.sin( rad ) );
		System.out.println( "cos(" + deg + ")=" + Math.cos( rad ) );
		System.out.println( "tan(" + deg + ")=" + Math.tan( rad ) );
	}
}

コンパイルソースコードが「ANSI」の場合

C:\talavax\javasample>javac -encoding sjis TriFunction.java

コンパイルソースコードが「UTF-8」の場合

C:\talavax\javasample>javac TriFunction.java

実行

C:\talavax\javasample>java TriFunction 60.0

60°のsin、cos、tanを求めます。

出力結果

■計算結果
sin(60.0)=0.8660254037768191
cos(60.0)=0.5000000000131974
tan(60.0)=1.732050807507921
ループ回数=35

■Mathクラスでの計算結果
sin(60.0)=0.8660254037844386
cos(60.0)=0.5000000000000001
tan(60.0)=1.7320508075688767