数学
数値微分
ここでは、f(x)をxで微分した値を数値計算で求める方法を紹介します。
f(x)によって、f'(x)を求めるのが難しい、または、不可能なことがあります。そのような場合に数値微分は有効です。
それでは、数値微分についてもう少し詳しく説明していきます。
直感的には、微分f'(x)は、関数f(x)の接線の傾きです。よって、傾きを求めるには、xを少しだけ増加させたときに、yがどれだけ増加するかを計算して、その結果から(yの増加分/xの増加分)を計算すれば、その値がf'(x)の近似値となります。
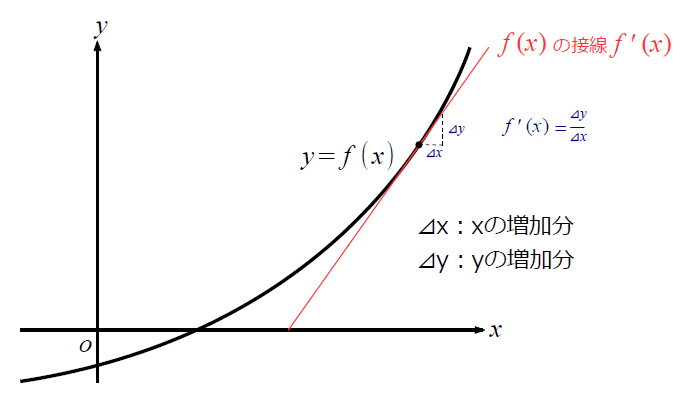
上の図からf'(x)の計算式は、以下のよう計算できます。
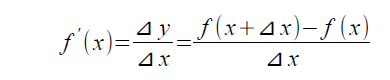
xの増加分の決め方は関数f(x)によっても変える必要があります。実際の微分では、限りなく0に近い値がxの増加分ですが、数値計算を行うときに使う変数には扱える数値の範囲があるため、オーバーフロー/アンダーフローしないように注意してxの増加分を決める必要があります。
以下の記事では、数値微分を使ったニュートン法を解説しています。興味がある方は、是非ご覧ください。
以上です。


