2020.12.16
数学
円周率πを計算で求める その2
以下がライプニッツの公式で、級数で表されます。
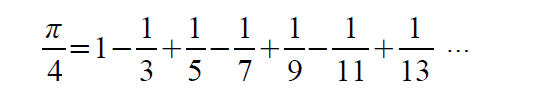
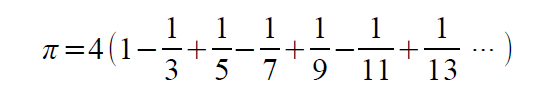
Javaソースコード - ライプニッツの公式でπを計算
LeibnizFormula.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061
public class LeibnizFormula { // 項の数termnumberを渡して円周率πを計算 static double LeibnizFormula( int termnumber ) { double sgn; // 符号 double pi; // 計算結果 double denom; // 分母 if ( 1 > termnumber ) return 0; // πの初期値に0.0を代入 pi = 0.0; // 符号の初期値に1を代入 sgn = 1.0; // 分母の初期値に1.0を代入 denom = 1.0; // π/4の計算 for ( int i = 1; i <= termnumber; i++ ) { // 項の値を計算（符号付） pi += sgn / denom; // 符号を反対にする sgn *= -1.0; // 分母に2を足す denom += 2.0; } // πの結果を戻す return pi * 4.0; } // メイン public static void main( String[] args ) { int termnum; // 項の数 double pi; // 計算結果 termnum = 100; pi = LeibnizFormula( termnum ); System.out.println( "項の数:" + termnum + " " + pi ); termnum = 1000; pi = LeibnizFormula( termnum ); System.out.println( "項の数:" + termnum + " " + pi ); termnum = 10000; pi = LeibnizFormula( termnum ); System.out.println( "項の数:" + termnum + " " + pi ); termnum = 100000; pi = LeibnizFormula( termnum ); System.out.println( "項の数:" + termnum + " " + pi ); termnum = 1000000; pi = LeibnizFormula( termnum ); System.out.println( "項の数:" + termnum + " " + pi ); } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis LeibnizFormula.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac LeibnizFormula.java
実行
C:\talavax\javasample>java LeibnizFormula
出力結果
項の数:100 3.1315929035585537 項の数:1000 3.140592653839794 項の数:10000 3.1414926535900345 項の数:100000 3.1415826535897198 項の数:1000000 3.1415916535897743
ただし、この公式は収束が遅く実用的ではありません。
実際の値に近づけるためには項の数を相当多くする必要があります。
ここからライプニッツの公式を計算するメソッドを説明していきます。
002 003 004
// 項の数termnumberを渡して円周率πを計算 static double LeibnizFormula( int termnumber ) {
static double LeibnizFormula( int termnumber )はライプニッツの公式で円周率πを計算するメソッドです。int型の引数termnumberは計算する項の数で、この数を大きくすると計算精度が高くなります。
005 006 007
double sgn; // 符号 double pi; // 計算結果 double denom; // 分母
計算で使う変数を宣言しています。
009
if ( 1 > termnumber ) return 0;
計算する項の数termnumberが１未満の場合は計算できないので、戻り値を0.0にしています。
011 012
// πの初期値に0.0を代入
pi = 0.0;
014 015
// 符号の初期値に1を代入
sgn = 1.0;
017 018
// 分母の初期値に1.0を代入
denom = 1.0;
020 021
// π/4の計算 for ( int i = 1; i <= termnumber; i++ ) {
022 023
// 項の値を計算（符号付）
pi += sgn / denom;
025 026
// 符号を反対にする
sgn *= -1.0;
符号を表す変数sgnに-1.0を掛けています。これで交互にプラスとマイナスが入れ替わります。
028 029
// 分母に2を足す
denom += 2.0;
分母を表す変数denomに2.0を足しています。
032 033
// πの結果を戻す return pi * 4.0;
Javaソースコード - ライプニッツの公式の項数を変えてπを計算
LeibnizFormula1.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036
public class LeibnizFormula1 { // メイン public static void main( String[] args ) { int termnum; // 項の数 double sgn; // 符号 double pi; // 計算結果 double denom; // 分母 // πの初期値に0.0を代入 pi = 0.0; // 符号の初期値に1を代入 sgn = 1.0; // 分母の初期値に1.0を代入 denom = 1.0; // 項の数を代入 termnum = 1000; // π計算 for ( int i = 1; i <= termnum; i++ ) { // 項の値を計算（符号付） pi += sgn / denom; // 符号を反対にする sgn *= -1.0; // 分母に2を足す denom += 2.0; // 結果を都度出力 System.out.println( i + " : " + pi * 4.0 ); } } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis LeibnizFormula1.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac LeibnizFormula1.java
実行
C:\talavax\javasample>java LeibnizFormula1
出力結果
1 : 4.0 2 : 2.666666666666667 3 : 3.466666666666667 4 : 2.8952380952380956 5 : 3.3396825396825403 6 : 2.9760461760461765 7 : 3.2837384837384844 8 : 3.017071817071818 9 : 3.2523659347188767 10 : 3.0418396189294032 11 : 3.232315809405594 12 : 3.058402765927333 13 : 3.2184027659273333 14 : 3.0702546177791854 15 : 3.208185652261944 16 : 3.079153394197428 17 : 3.200365515409549 18 : 3.0860798011238346 19 : 3.1941879092319425 20 : 3.09162380666784 21 : 3.189184782277596 22 : 3.0961615264636424 23 : 3.1850504153525314 24 : 3.099944032373808 25 : 3.1815766854350325
公式に関するコンテンツ
「公式」に関係があるコンテンツをまとめています。
関連コンテンツ
広告
