2024.10.30
２つのサイコロの出目の和の確率
はじめに
出目の和の確率(理論値)の計算方法
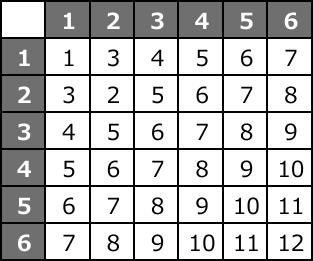
この表から、和ごとの出現個数をまとめたものが以下の表です。
| 出目の和 | 出現個数 |
|---|---|
| 2 | 1個 |
| 3 | 2個 |
| 4 | 3個 |
| 5 | 4個 |
| 6 | 5個 |
| 7 | 6個 |
| 8 | 5個 |
| 9 | 4個 |
| 10 | 3個 |
| 11 | 2個 |
| 12 | 1個 |
和の出現個数を全組み合わせで割ると、出現確率の理論値が計算できます。
下の表の「出現率(%)」は出現確率の理論値を表したもので、「出現個数」を36で割った値です。
この「出現率(%)」が、２つのサイコロを振ったときの出目の和の確率(理論値)となります。
| 出目の和 | 出現個数 | 出現率(%) |
|---|---|---|
| 2 | 1個 | 2.78 |
| 3 | 2個 | 5.56 |
| 4 | 3個 | 8.33 |
| 5 | 4個 | 11.11 |
| 6 | 5個 | 13.89 |
| 7 | 6個 | 16.67 |
| 8 | 5個 | 13.89 |
| 9 | 4個 | 11.11 |
| 10 | 3個 | 8.33 |
| 11 | 2個 | 5.56 |
| 12 | 1個 | 2.78 |
Javaソースコード - 理論値の確認
Dice2_1.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020
public class Dice2_1 { public static void main(String[] args) { // 出目の回数(2-12) int numbers[] = new int[ 11 ]; // 出目1と出目2の全ての組み合わせ for ( int deme1 = 1; deme1 <= 6; ++ deme1 ) { for ( int deme2 = 1; deme2 <= 6; ++ deme2 ) { // ２つの出目の和の配列に1を足す ++ numbers[ deme1 + deme2 - 2 ]; } } // 結果を表示 System.out.println( "２つサイコロの和の理論上の確率" ); for ( int i = 2; i <= 12; ++ i ) { System.out.println( i + "になる確率 : " + numbers[ i - 2 ] + "/36 " + (double)numbers[ i - 2 ] / 36.0 * 100.0 + "％" ); } } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis Dice2_1.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac Dice2_1.java
実行
C:\talavax\javasample>java Dice2_1
実行結果
２つサイコロの和の理論上の確率 2になる確率 : 1/36 2.7777777777777777％ 3になる確率 : 2/36 5.555555555555555％ 4になる確率 : 3/36 8.333333333333332％ 5になる確率 : 4/36 11.11111111111111％ 6になる確率 : 5/36 13.88888888888889％ 7になる確率 : 6/36 16.666666666666664％ 8になる確率 : 5/36 13.88888888888889％ 9になる確率 : 4/36 11.11111111111111％ 10になる確率 : 3/36 8.333333333333332％ 11になる確率 : 2/36 5.555555555555555％ 12になる確率 : 1/36 2.7777777777777777％
ここからソースコードを順番に解説していきます。
001
public class Dice2_1 {
クラス名を、Dice2_1としています。
002
public static void main(String[] args) {
このmainメソッドからプログラムを実行します。
003 004
// 出目の回数(2-12) int numbers[] = new int[ 11 ];
サイコロ２つの和の個数を格納するint型の配列numbersを作成しています。
和の最小は「2」、最大は「12」なので、「2」から「12」の11個の和の個数が格納できる配列を作成してます。
作成直後のnumbers配列の値は、全て0になっています。
006 007 008
// 出目1と出目2の全ての組み合わせ for ( int deme1 = 1; deme1 <= 6; ++ deme1 ) { for ( int deme2 = 1; deme2 <= 6; ++ deme2 ) {
009 010
// ２つの出目の和の配列に1を足す
++ numbers[ deme1 + deme2 - 2 ];
変数deme1と変数deme2を足した値から２を引いた値を、配列numbersの添え字にして、インクリメント(1を足す)しています。
和が「2」の個数はnumbers[0]、「12」の個数はnumbers[10]に格納していくようにしているので、和のから２を引いた値を添え字にしています。
014 015
// 結果を表示 System.out.println( "２つサイコロの和の理論上の確率" );
016 017 018
for ( int i = 2; i <= 12; ++ i ) { System.out.println( i + "になる確率 : " + numbers[ i - 2 ] + "/36 " + (double)numbers[ i - 2 ] / 36.0 * 100.0 + "％" ); }
「2」から「12」の和の出現確率をコンソール出力しています。
for文を使って変数iを２から１２に変化させ、和の個数を格納した配列numbers[ i - 2 ]の値、numbers[ i - 2 ]から計算した確率(%)を出力しています。
Javaソースコード - 乱数を使った確認
Dice2_2.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027
public class Dice2_2 { public static void main(String[] args) { // サイコロを振る回数 int count = 100000; // 出目の回数(2-12) int numbers[] = new int[ 11 ]; // 100000回乱数を発生（サイコロを振る） for ( int i = 1; i <= count; ++ i ) { // １つ目のサイコロ 1から6の乱数を発生 int deme1 = (int)( Math.random() * 6.0 ) + 1; // ２つ目のサイコロ 1から6の乱数を発生 int deme2 = (int)( Math.random() * 6.0 ) + 1; // ２つの出目の和の配列に1を足す ++ numbers[ deme1 + deme2 - 2 ]; } // 結果を表示 System.out.println( "サイコロを振った回数:" + count + "回" ); for ( int i = 2; i <= 12; ++ i ) { System.out.println( i + "になる確率 : " + (double)numbers[ i - 2 ] / (double)count * 100.0 + "％" ); } } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis Dice2_2.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac Dice2_2.java
実行
C:\talavax\javasample>java Dice2_2
実行結果
サイコロを振った回数:100000回 2になる確率 : 2.686％ 3になる確率 : 5.5329999999999995％ 4になる確率 : 8.43％ 5になる確率 : 11.076％ 6になる確率 : 13.869000000000002％ 7になる確率 : 16.853％ 8になる確率 : 13.923％ 9になる確率 : 11.021％ 10になる確率 : 8.315999999999999％ 11になる確率 : 5.539000000000001％ 12になる確率 : 2.754％
理論値に近い確率が出力されています。
実行結果は毎回違いますが、理論値に近い確率が出力されます。
ここからソースコードを順番に解説していきます。
001
public class Dice2_2 {
クラス名を、Dice2_2としています。
002
public static void main(String[] args) {
このmainメソッドからプログラムを実行します。
003 004
// サイコロを振る回数 int count = 100000;
006 007
// 出目の回数(2-12) int numbers[] = new int[ 11 ];
サイコロ２つの和の個数を格納するint型の配列numbersを作成しています。
和の最小は「2」、最大は「12」なので、「2」から「12」の11個の和の個数が格納できる配列を作成してます。
作成直後のnumbers配列の値は、全て0になっています。
009 010
// 100000回乱数を発生（サイコロを振る） for ( int i = 1; i <= count; ++ i ) {
011 012 013 014 015
// １つ目のサイコロ 1から6の乱数を発生 int deme1 = (int)( Math.random() * 6.0 ) + 1; // ２つ目のサイコロ 1から6の乱数を発生 int deme2 = (int)( Math.random() * 6.0 ) + 1;
Math.randomメソッド
public static double Math.random()
・乱数を返します。 パラメータ なし 戻り値 0.0以上、1.0未満の乱数
Math.random()の戻り値は、0.0以上で1.0未満です。
したがって、(int)( Math.random() * 6.0 )の値は、整数の０から５になります。
( Math.random() * 6.0 )の値はdouble型です。この式の頭に(int)を付けてint型に型キャストするとdouble型の値の小数部が切り捨てられるので０から５になります。
(int)( Math.random() * 6.0 )に１を足すことで１から６の乱数を作成しています。
017 018
// ２つの出目の和の配列に1を足す
++ numbers[ deme1 + deme2 - 2 ];
変数deme1と変数deme2を足した値から２を引いた値を、配列numbersの添え字にして、インクリメント(1を足す)しています。
和が「2」の個数はnumbers[0]、「12」の個数はnumbers[10]に格納していくようにしているので、和のから２を引いた値を添え字にしています。
021 022
// 結果を表示 System.out.println( "サイコロを振った回数:" + count + "回" );
023 024
for ( int i = 2; i <= 12; ++ i ) { System.out.println( i + "になる確率 : " + (double)numbers[ i - 2 ] / (double)count * 100.0 + "％" );
「2」から「12」の和の出現確率をコンソール出力しています。
for文を使って変数iを２から１２に変化させ、和の個数を格納した配列numbers[ i - 2 ]の値、numbers[ i - 2 ]から計算した確率(%)を出力しています。
以上です。
関連コンテンツ
広告
