2022.12.16
2025.01.23
バビロニアの平方根
はじめに
バビロニアの平方根は、高度な数学技術を持っていた古代バビロニア人により導き出された平方根の計算方法です。「バビロニア人の方法」、「バビロニアンメソッド」とも呼ばれます。
この方法で、以下の式のaを与えてxを求めることができます。

バビロニアの平方根の計算式は、
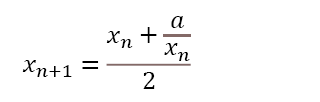
です。
この計算式に任意のaを与えて新しいxを計算します。この計算を繰り返していき、計算後のxと計算前のxの差がなくなったときのxが求める値となります。
この式は、xとa/xの平均値を計算しています。
直観的なこの式の解釈ですが、以下の理由でxがaの平方根(√a)に近づいていくと考えられます。
xが√aの場合、a/xはa/√a=√a=xとなります。よって、xとa/x(=x)の平均値はxになります。
xが√aより小さい場合、a/xは√aより大きい値になります。(x < √a < a/x)
xが√aより大きい場合、a/xは√aより小さい値になります。(a/x < √a < x)
このように、xとa/xの間に√aの値があることがわかります。
xとa/xの平均値を新しいxとして計算するとxとa/xの差が小さくなるので、これを繰り返していくとxが√aに近づいていきます。
Javaソースコード
0から100の平方根をバビロニアの平方根の計算で求めてコンソール出力するソースコードです。また、比較のためにJavaのMath.sqrtメソッドの計算も上下に並べて出力します。
BabylonianSqrt.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071 072 073 074 075 076 077 078 079 080 081
public class BabylonianSqrt { // aの平方根に近い整数を求める private static int get_x0( double a ) { // aが0以下の場合、xを戻す if ( 0.0 >= a ) return (int)a; // 変数の宣言 int x0; // 解を格納 double sqr0 = 0.0; // 1つ前のiの2乗を格納 // 無限ループを作成し、iを1から1ずつ増やす for ( int i = 1; ; i++ ) { // iの2乗の値を格納 double sqr1 = (double)( i * i ); // sqr1がa以上になったら if ( sqr1 >= a ) { // aに近い値整数を判定 if ( ( sqr1 - a ) > ( a - sqr0 ) ) x0 = i - 1; else x0 = i; // ループを抜ける break; } // 1つ前のiの2乗の値を格納 sqr0 = sqr1; } return x0; } // バビロニア平方根 private static double babylonian_method( double a ) { // 計算が収束したとみなす値 double eps = 0.0000000001; // aが0以下の場合、aを戻す if ( 0.0 >= a ) return a; // 計算の初期値を求める double x = (double)get_x0( a ); // 1つ前の計算結果を保持 double prev_x = x; // ループ回数の上限を100万回にする for ( int i = 0; i < 1000000; i++ ) { // 計算 x = ( x + a / x ) / 2.0; // 1つ前の計算結果と差がepsより小さい場合、ループを抜ける if ( Math.abs( x - prev_x ) < eps ) break; // 1つ前の計算結果を保持 prev_x = x; } // 解を戻す return x; } // メイン public static void main( String[] args ) { for ( int i = 0; i <= 100; i++ ) { // 結果出力 System.out.println( i + "の平方根" ); System.out.println( "バビロニア平方根:" + babylonian_method( (double)i ) ); System.out.println( "Math.Sqrtで計算 :" + Math.sqrt( (double)i ) ); // 改行 System.out.println(); } } }
実行結果
実行
java BabylonianSqrt
出力結果
0の平方根 バビロニア平方根:0.0 Math.Sqrtで計算 :0.0 1の平方根 バビロニア平方根:1.0 Math.Sqrtで計算 :1.0 2の平方根 バビロニア平方根:1.414213562373095 Math.Sqrtで計算 :1.4142135623730951 3の平方根 バビロニア平方根:1.7320508075688772 Math.Sqrtで計算 :1.7320508075688772 4の平方根 バビロニア平方根:2.0 Math.Sqrtで計算 :2.0 5の平方根 バビロニア平方根:2.23606797749979 Math.Sqrtで計算 :2.23606797749979 6の平方根 バビロニア平方根:2.449489742783178 Math.Sqrtで計算 :2.449489742783178 7の平方根 バビロニア平方根:2.6457513110645907 Math.Sqrtで計算 :2.6457513110645907 8の平方根 バビロニア平方根:2.82842712474619 Math.Sqrtで計算 :2.8284271247461903 9の平方根 バビロニア平方根:3.0 Math.Sqrtで計算 :3.0 10の平方根 バビロニア平方根:3.162277660168379 Math.Sqrtで計算 :3.1622776601683795 11の平方根 バビロニア平方根:3.3166247903554 Math.Sqrtで計算 :3.3166247903554 12の平方根 バビロニア平方根:3.4641016151377544 Math.Sqrtで計算 :3.4641016151377544 13の平方根 バビロニア平方根:3.6055512754639896 Math.Sqrtで計算 :3.605551275463989 14の平方根 バビロニア平方根:3.7416573867739413 Math.Sqrtで計算 :3.7416573867739413 15の平方根 バビロニア平方根:3.872983346207417 Math.Sqrtで計算 :3.872983346207417 16の平方根 バビロニア平方根:4.0 Math.Sqrtで計算 :4.0 17の平方根 バビロニア平方根:4.123105625617661 Math.Sqrtで計算 :4.123105625617661 18の平方根 バビロニア平方根:4.242640687119286 Math.Sqrtで計算 :4.242640687119285 19の平方根 バビロニア平方根:4.358898943540673 Math.Sqrtで計算 :4.358898943540674 20の平方根 バビロニア平方根:4.47213595499958 Math.Sqrtで計算 :4.47213595499958 21の平方根 バビロニア平方根:4.58257569495584 Math.Sqrtで計算 :4.58257569495584 22の平方根 バビロニア平方根:4.69041575982343 Math.Sqrtで計算 :4.69041575982343 23の平方根 バビロニア平方根:4.795831523312719 Math.Sqrtで計算 :4.795831523312719 24の平方根 バビロニア平方根:4.898979485566356 Math.Sqrtで計算 :4.898979485566356 25の平方根 バビロニア平方根:5.0 Math.Sqrtで計算 :5.0 26の平方根 バビロニア平方根:5.0990195135927845 Math.Sqrtで計算 :5.0990195135927845 27の平方根 バビロニア平方根:5.196152422706632 Math.Sqrtで計算 :5.196152422706632 28の平方根 バビロニア平方根:5.291502622129181 Math.Sqrtで計算 :5.291502622129181 29の平方根 バビロニア平方根:5.385164807134505 Math.Sqrtで計算 :5.385164807134504 30の平方根 バビロニア平方根:5.477225575051661 Math.Sqrtで計算 :5.477225575051661 31の平方根 バビロニア平方根:5.567764362830022 Math.Sqrtで計算 :5.5677643628300215 32の平方根 バビロニア平方根:5.65685424949238 Math.Sqrtで計算 :5.656854249492381 33の平方根 バビロニア平方根:5.744562646538029 Math.Sqrtで計算 :5.744562646538029 34の平方根 バビロニア平方根:5.830951894845301 Math.Sqrtで計算 :5.830951894845301 35の平方根 バビロニア平方根:5.916079783099616 Math.Sqrtで計算 :5.916079783099616 36の平方根 バビロニア平方根:6.0 Math.Sqrtで計算 :6.0 37の平方根 バビロニア平方根:6.08276253029822 Math.Sqrtで計算 :6.082762530298219 38の平方根 バビロニア平方根:6.164414002968977 Math.Sqrtで計算 :6.164414002968976 39の平方根 バビロニア平方根:6.244997998398398 Math.Sqrtで計算 :6.244997998398398 40の平方根 バビロニア平方根:6.324555320336758 Math.Sqrtで計算 :6.324555320336759 41の平方根 バビロニア平方根:6.4031242374328485 Math.Sqrtで計算 :6.4031242374328485 42の平方根 バビロニア平方根:6.48074069840786 Math.Sqrtで計算 :6.48074069840786 43の平方根 バビロニア平方根:6.557438524302 Math.Sqrtで計算 :6.557438524302 44の平方根 バビロニア平方根:6.6332495807108 Math.Sqrtで計算 :6.6332495807108 45の平方根 バビロニア平方根:6.708203932499369 Math.Sqrtで計算 :6.708203932499369 46の平方根 バビロニア平方根:6.782329983125268 Math.Sqrtで計算 :6.782329983125268 47の平方根 バビロニア平方根:6.855654600401044 Math.Sqrtで計算 :6.855654600401044 48の平方根 バビロニア平方根:6.928203230275509 Math.Sqrtで計算 :6.928203230275509 49の平方根 バビロニア平方根:7.0 Math.Sqrtで計算 :7.0 50の平方根 バビロニア平方根:7.0710678118654755 Math.Sqrtで計算 :7.0710678118654755 51の平方根 バビロニア平方根:7.14142842854285 Math.Sqrtで計算 :7.14142842854285 52の平方根 バビロニア平方根:7.211102550927979 Math.Sqrtで計算 :7.211102550927978 53の平方根 バビロニア平方根:7.280109889280518 Math.Sqrtで計算 :7.280109889280518 54の平方根 バビロニア平方根:7.3484692283495345 Math.Sqrtで計算 :7.3484692283495345 55の平方根 バビロニア平方根:7.416198487095663 Math.Sqrtで計算 :7.416198487095663 56の平方根 バビロニア平方根:7.483314773547883 Math.Sqrtで計算 :7.483314773547883 57の平方根 バビロニア平方根:7.54983443527075 Math.Sqrtで計算 :7.54983443527075 58の平方根 バビロニア平方根:7.615773105863909 Math.Sqrtで計算 :7.615773105863909 59の平方根 バビロニア平方根:7.681145747868609 Math.Sqrtで計算 :7.681145747868608 60の平方根 バビロニア平方根:7.745966692414834 Math.Sqrtで計算 :7.745966692414834 61の平方根 バビロニア平方根:7.810249675906654 Math.Sqrtで計算 :7.810249675906654 62の平方根 バビロニア平方根:7.874007874011811 Math.Sqrtで計算 :7.874007874011811 63の平方根 バビロニア平方根:7.937253933193771 Math.Sqrtで計算 :7.937253933193772 64の平方根 バビロニア平方根:8.0 Math.Sqrtで計算 :8.0 65の平方根 バビロニア平方根:8.06225774829855 Math.Sqrtで計算 :8.06225774829855 66の平方根 バビロニア平方根:8.12403840463596 Math.Sqrtで計算 :8.12403840463596 67の平方根 バビロニア平方根:8.18535277187245 Math.Sqrtで計算 :8.18535277187245 68の平方根 バビロニア平方根:8.246211251235321 Math.Sqrtで計算 :8.246211251235321 69の平方根 バビロニア平方根:8.306623862918075 Math.Sqrtで計算 :8.306623862918075 70の平方根 バビロニア平方根:8.366600265340756 Math.Sqrtで計算 :8.366600265340756 71の平方根 バビロニア平方根:8.426149773176359 Math.Sqrtで計算 :8.426149773176359 72の平方根 バビロニア平方根:8.485281374238571 Math.Sqrtで計算 :8.48528137423857 73の平方根 バビロニア平方根:8.544003745317532 Math.Sqrtで計算 :8.54400374531753 74の平方根 バビロニア平方根:8.602325267042627 Math.Sqrtで計算 :8.602325267042627 75の平方根 バビロニア平方根:8.660254037844386 Math.Sqrtで計算 :8.660254037844387 76の平方根 バビロニア平方根:8.717797887081346 Math.Sqrtで計算 :8.717797887081348 77の平方根 バビロニア平方根:8.77496438739212 Math.Sqrtで計算 :8.774964387392123 78の平方根 バビロニア平方根:8.831760866327848 Math.Sqrtで計算 :8.831760866327848 79の平方根 バビロニア平方根:8.888194417315589 Math.Sqrtで計算 :8.888194417315589 80の平方根 バビロニア平方根:8.94427190999916 Math.Sqrtで計算 :8.94427190999916 81の平方根 バビロニア平方根:9.0 Math.Sqrtで計算 :9.0 82の平方根 バビロニア平方根:9.055385138137417 Math.Sqrtで計算 :9.055385138137417 83の平方根 バビロニア平方根:9.1104335791443 Math.Sqrtで計算 :9.1104335791443 84の平方根 バビロニア平方根:9.16515138991168 Math.Sqrtで計算 :9.16515138991168 85の平方根 バビロニア平方根:9.219544457292887 Math.Sqrtで計算 :9.219544457292887 86の平方根 バビロニア平方根:9.273618495495704 Math.Sqrtで計算 :9.273618495495704 87の平方根 バビロニア平方根:9.327379053088816 Math.Sqrtで計算 :9.327379053088816 88の平方根 バビロニア平方根:9.38083151964686 Math.Sqrtで計算 :9.38083151964686 89の平方根 バビロニア平方根:9.433981132056605 Math.Sqrtで計算 :9.433981132056603 90の平方根 バビロニア平方根:9.486832980505138 Math.Sqrtで計算 :9.486832980505138 91の平方根 バビロニア平方根:9.539392014169456 Math.Sqrtで計算 :9.539392014169456 92の平方根 バビロニア平方根:9.591663046625438 Math.Sqrtで計算 :9.591663046625438 93の平方根 バビロニア平方根:9.643650760992955 Math.Sqrtで計算 :9.643650760992955 94の平方根 バビロニア平方根:9.695359714832659 Math.Sqrtで計算 :9.695359714832659 95の平方根 バビロニア平方根:9.746794344808965 Math.Sqrtで計算 :9.746794344808963 96の平方根 バビロニア平方根:9.797958971132712 Math.Sqrtで計算 :9.797958971132712 97の平方根 バビロニア平方根:9.848857801796104 Math.Sqrtで計算 :9.848857801796104 98の平方根 バビロニア平方根:9.899494936611665 Math.Sqrtで計算 :9.899494936611665 99の平方根 バビロニア平方根:9.9498743710662 Math.Sqrtで計算 :9.9498743710662 100の平方根 バビロニア平方根:10.0 Math.Sqrtで計算 :10.0
Javaソースコードの解説
001
public class BabylonianSqrt {
クラス名を、BabylonianSqrtとしています。
002 003
// aの平方根に近い整数を求める private static int get_x0( double a )
005 006
// aが0以下の場合、xを戻す if ( 0.0 >= a ) return (int)a;
008 009 010
// 変数の宣言 int x0; // 解を格納 double sqr0 = 0.0; // 1つ前のiの2乗を格納
int型の変数x0は、aの平方根に近いを整数値を格納する変数です。double型のsqr0は、1つ前のiの2乗を格納する変数です。sqr0がdouble型なのは、double型の引数aとの計算処理を行うためです。
012 013
// 無限ループを作成し、iを1から1ずつ増やす for ( int i = 1; ; i++ ) {
014 015
// iの2乗の値を格納 double sqr1 = (double)( i * i );
017 018
// sqr1がa以上になったら
if ( sqr1 >= a ) {
019 020 021 022 023
// aに近い値整数を判定
if ( ( sqr1 - a ) > ( a - sqr0 ) )
x0 = i - 1;
else
x0 = i;
この処理の時点での変数aの値は、sqr0以上、sqr1以下です。(sqr0≦a≦sqr1)
( sqr1 - a )が( a - sqr0 )より大きければ、sqr0の方がaに近いのでsqr0の元の値( i - 1 )をx0に代入しています。
sqr1の方がaに近い場合は、sqr1の元の値iをx0に代入しています。
025 026
// ループを抜ける break;
029 030
// 1つ前のiの2乗の値を格納
sqr0 = sqr1;
sqr1の値を1つ目のiの2乗を格納しているsqr0に代入しています。
033
return x0;
037 038 039
// バビロニア平方根 private static double babylonian_method( double a ) {
040 041
// 計算が収束したとみなす値 double eps = 0.0000000001;
043 044
// aが0以下の場合、aを戻す
if ( 0.0 >= a ) return a;
046 047
// 計算の初期値を求める double x = (double)get_x0( a );
049 050
// 1つ前の計算結果を保持 double prev_x = x;
052 053
// ループ回数の上限を100万回にする for ( int i = 0; i < 1000000; i++ ) {
054 055
// 計算
x = ( x + a / x ) / 2.0;
057 058
// 1つ前の計算結果と差がepsより小さい場合、ループを抜ける
if ( Math.abs( x - prev_x ) < eps ) break;
060 061
// 1つ前の計算結果を保持
prev_x = x;
直前で計算した値xを1つ前の計算結果prev_xに代入しています。
064 065
// 解を戻す return x;
069 070
// メイン public static void main( String[] args ) {
071
for ( int i = 0; i <= 100; i++ ) {
072 073
// 結果出力 System.out.println( i + "の平方根" );
074
System.out.println( "バビロニア平方根:" + babylonian_method( (double)i ) );
075
System.out.println( "Math.Sqrtで計算 :" + Math.sqrt( (double)i ) );
Math.sqrtメソッド
public static double Math.sqrt( double a )
・引数aで指定した数値の平方根を返します。 パラメータ a : 平方根を求める数値 戻り値 aの平方根
077 078
// 改行
System.out.println();
ニュートン法と計算式が一致
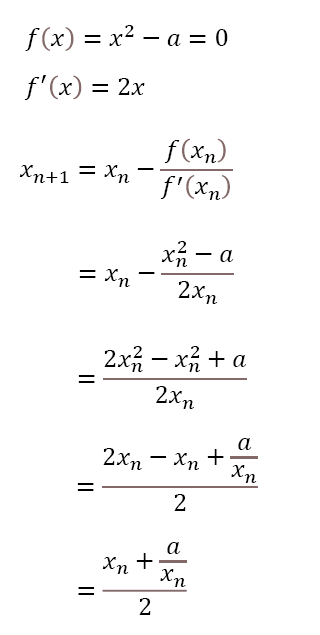
以上です。
平方根に関するコンテンツ
「平方根」に関係があるコンテンツをまとめています。


