ゆるゆるプログラミング

１＋２＋３＋ … ＋ｎを計算する公式は、

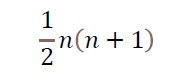
です。ｎを公式に代入すると結果が得られます。

例えばｎ＝１０の場合、１０÷２×（１０＋１）＝５×１１＝５５になります。

それでは、この公式を導いていきましょう。

まず、以下の図を見てください。面積１の青色の正方形を並べています。ｎ＝５とｎ＝６の場合の和を計算する並べ方です。

このように並べた全ての青色の正方形の面積の合計値が１から５の和、１から６の和となります。

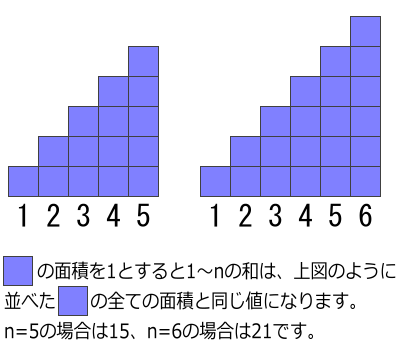
次に、面積を計算する式を作っていきます。

並べた正方形の左下から右上に直線を引いたときに（下図）、線の下に１つの三角形（下図のオレンジ色の部分）と、線の上にｎ個の三角形（下図の赤色の部分）が作られます。これら三角形の面積はｎを使った式で表すことができます。

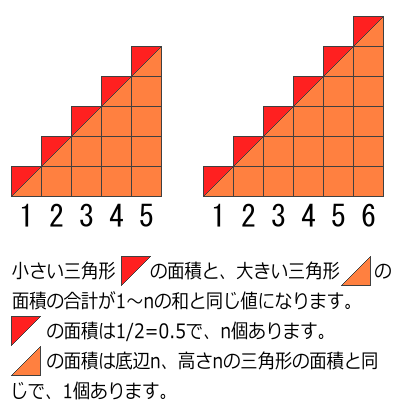
オレンジ色の部分は、底辺の長さｎで高さがｎの三角形なので、（底辺×高さ÷２）＝ｎ×ｎ÷２で面積を計算することができます。赤色の部分の三角形は、面積１の正方形を半分にしたものなので面積は１／２です。この赤色の三角形はｎ個あるので、赤色の三角形の面積の合計は、（１／２×ｎ）→ｎ／２となります。

このオレンジと赤色の三角形の面積の合計が、全ての正方形の面積です。式で書くと以下のようになります。

面積を利用して計算した式が、和の公式と同じになりました。

以上です。