数学
ヘロンの方式
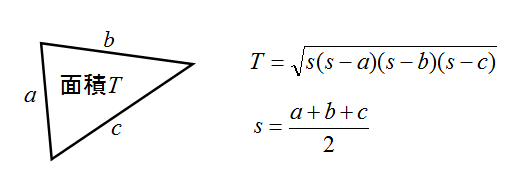
Javaソースコード
Heron.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066
public class Heron { public static void main( String[] args ) { // 変数の宣言 double a, b, c; // 3辺の長さ double t; // 面積 // 入力した引数が3つ以上かを調べる if ( 3 >args.length ) { // 入力した引数が3つ未満の場合、使用方法を表示する System.out.println( "Heron [辺長1] [辺長2] [辺長3]" ); return; } // 引数をdouble型に変換し、長さに代入 try { // args[0],args[1],args[2]を数値に変換 a = Double.valueOf( args[ 0 ] ); b = Double.valueOf( args[ 1 ] ); c = Double.valueOf( args[ 2 ] ); } catch( NumberFormatException ne ) { // args[0],args[1],args[2]のどれかが数字ではない System.out.println( "辺の長さの取得に失敗しました" ); return; } // 面積を計算 t = herons_formula( a, b, c ); if ( 0.0 > t ) { System.out.println( "面積の計算に失敗しました" ); } else { System.out.println( "辺1の長さ="+ a ); System.out.println( "辺2の長さ="+ b ); System.out.println( "辺3の長さ="+ c ); System.out.println( "面積="+ t ); } } // 3角形の3辺の長さa,b,cから面積を計算するメソッド private static double herons_formula( double a, double b, double c ) { double s; // s = ( a + b + c ) / 2 double t; // 面積 double d; // 作業用変数 // 3辺のどれか1つでも0より小さければ-1.0を返す if ( ( 0.0 > a ) || ( 0.0 > b ) || ( 0.0 > c ) ) return -1.0; // sを計算 s = ( a + b + c ) / 2.0; // s(s-a)(s-b)(s-c)を計算し、マイナスになれば-1.0を返す d = s * ( s - a ) * ( s - b ) * ( s - c ); if ( 0.0 > d ) return -1.0; // 面積tを計算 t = Math.sqrt( d ); // 計算した面積tを返す return t; } }
実行結果
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis Heron.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac Heron.java
Heronを実行
C:\talavax\javasample>java Heron 5 12 9
辺1の長さ=5.0 辺2の長さ=12.0 辺3の長さ=9.0 面積=20.396078054371138
Javaソースコードの解説
ここからは、このソースコードを上から順番に解説していきます。
001
public class Heron {
クラス名を、Heronとしています。
002
public static void main( String[] args ) {
003 004 005
// 変数の宣言 double a, b, c; // 3辺の長さ double t; // 面積
007 008 009 010 011 012
// 入力した引数が3つ以上かを調べる if ( 3 >args.length ) { // 入力した引数が3つ未満の場合、使用方法を表示する System.out.println( "Heron [辺長1] [辺長2] [辺長3]" ); return; }
014 015 016 017 018 019 020 021 022 023 024 025 026
// 引数をdouble型に変換し、長さに代入 try { // args[0],args[1],args[2]を数値に変換 a = Double.valueOf( args[ 0 ] ); b = Double.valueOf( args[ 1 ] ); c = Double.valueOf( args[ 2 ] ); } catch( NumberFormatException ne ) { // args[0],args[1],args[2]のどれかが数字ではない System.out.println( "辺の長さの取得に失敗しました" ); return; }
try { ~ } catchは、失敗する可能性がある処理を波括弧で囲み、その処理に失敗したときにcatch { ~ }の波括弧で囲まれた処理を実行するということです。この場合は、与えられた引数が数値でなかったり、doubleの範囲を超えた引数が与えられたことが原因で処理が失敗する可能性があります。処理が失敗するとreturnによってmainメソッドを抜けるようにしています。
029 030 031 032 033 034 035 036 037 038 039
// 面積を計算 t = herons_formula( a, b, c ); if ( 0.0 > t ) { System.out.println( "面積の計算に失敗しました" ); } else { System.out.println( "辺1の長さ="+ a ); System.out.println( "辺2の長さ="+ b ); System.out.println( "辺3の長さ="+ c ); System.out.println( "面積="+ t ); }
後で説明するherons_formulaメソッドに3辺の長さa,b,cを渡して面積を計算します。herons_formulaメソッドの戻り値がマイナスの場合は、計算に失敗していることを表しているので、エラーメッセージを表示しています。面積計算に成功した場合は、メッセージを表示しています。
043 044
// 3角形の3辺の長さa,b,cから面積を計算するメソッド private static double herons_formula( double a, double b, double c )
046 047 048
double s; // s = ( a + b + c ) / 2 double t; // 面積 double d; // 作業用変数
050 051
// 3辺のどれか1つでも0より小さければ-1.0を返す
if ( ( 0.0 > a ) || ( 0.0 > b ) || ( 0.0 > c ) ) return -1.0;
与えられた3つの引数のうち1つでも0.0より小さい場合は、エラーとして-1.0を返しています。
053 054
// sを計算
s = ( a + b + c ) / 2.0;
ヘロンの公式で使うsを計算しています。
056 057 058
// s(s-a)(s-b)(s-c)を計算し、マイナスになれば-1.0を返す
d = s * ( s - a ) * ( s - b ) * ( s - c );
if ( 0.0 > d ) return -1.0;
s,a,b,cをヘロンの公式の平方根に渡す値dを計算しています。これは、平方根を計算するMath.sqrtメソッドにマイナスの値を渡さないようするためです。値がマイナスであれば-1.0を返すようにしています。
060 061
// 面積tを計算
t = Math.sqrt( d );
Math.sqrtメソッド
public static double Math.sqrt( double a )
・引数aで指定した数値の平方根を返します。 パラメータ a : 平方根を求める数値 戻り値 aの平方根
063 064
// 計算した面積tを返す return t;
以上です。


