2019.05.24
2025.03.18
ニュートン法で平方根 その3
はじめに
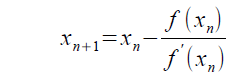
ニュートン法は、反復計算でf(x)=0のxの解を見つけていく方法ですが、解が見つからない場合に計算が収束せずに処理が終了できないことがあります。
メソッドの中でニュートン法を使い計算値を得ようとする場合は、解が得られない場合でも、処理を終了させて何かしらの値を戻す必要があります。このあたりのことをニュートン法で平方根を計算するメソッドのソースコードで詳しく説明します。
関数をf(x)=x2-aとし、f(x)=0となるxを求めることで、aの平方根を計算します。
この式は、以下の手順で導いています。
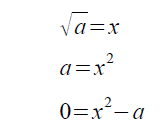
Javaソースコード
以下がそのJavaソースコードです。
NewtonsMethod.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066
public class NewtonsMethod { // f(x)=x^2-a static double f( double x, double a ) { return x * x - a; } // f(x)の微分f'(x) - 接線の傾き static double df( double x ) { return 2 * x; } // ニュートン法 漸化式 static double newtons( double x, double a ) { return x - f( x, a ) / df( x ); } // ニュートン法で平方根を計算するメソッド static double sqrt( double a ) { // 変数の宣言 double e = 0.000001; // 収束の判定値 double x; // 計算値を格納 double x_ans; // 1つ前の計算値 // aが0.0以下の場合、そのままのaの値を戻す if ( 0.0 >= a ) return a; // 初期値を代入 x_ans = 10000.0; // 5000回のループ for ( int i = 1; i <= 5000; ++ i ) { // ニュートン法で計算 x = newtons( x_ans, a ); // 収束の判定 if ( e > Math.abs( x - x_ans ) ) return Math.abs( x ); // 最新の計算結果を次の計算結果に代入 x_ans = x; } // 収束しなかった場合、マイナスの値を戻す return -1.0; } // メイン public static void main(String[] args) { // 変数の宣言 double a; // 平方根を求める値を代入 a = 77.7 * 77.7; // 結果の表示 System.out.println( a + "の平方根: " + sqrt( a ) ); } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis NewtonsMethod.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac NewtonsMethod.java
実行
C:\talavax\javasample>java NewtonsMethod
実行結果
6037.290000000001の平方根: 77.7
平方根の計算結果が77.7になっています。
Javaソースコードの解説
ここからは、Javaソースコードを順番に説明していきます。
001
public class NewtonsMethod {
002 003 004 005 006
// f(x)=x^2-a static double f( double x, double a ) { return x * x - a; }
009 010 011 012 013
// f(x)の微分f'(x) - 接線の傾き static double df( double x ) { return 2 * x; }
f(x)の微分式f'(x)を計算するメソッドです。
016 017 018 019 020
// ニュートン法 漸化式 static double newtons( double x, double a ) { return x - f( x, a ) / df( x ); }
023 024 025
// ニュートン法で平方根を計算するメソッド static double sqrt( double a ) {
026 027 028 029
// 変数の宣言 double e = 0.000001; // 収束の判定値 double x; // 計算値を格納 double x_ans; // 1つ前の計算値
031 032
// aが0.0以下の場合、そのままのaの値を戻す
if ( 0.0 >= a ) return a;
引数で渡された値aが0.0以下の場合、aの値をそのままメソッドの戻り値にしています。a=0.0の平方根は0.0なので計算の必要がありません。また、aが0.0未満の場合には、平方根の計算ができないためaの値をそのまま戻しています。これにより、このメソッドでは戻り値が0.0未満のときに計算エラーと判断できるようにしています。
034 035
// 初期値を代入
x_ans = 10000.0;
計算の初期値に10000.0を代入しています。この値は任意です。、
037 038
// 5000回のループ for ( int i = 1; i <= 5000; ++ i ) {
for文で5000回のループを作っています。これは5000回の計算を行った結果、計算値が収束しなかったら処理を強制終了させるものです。ループを5000回にしていることについては深い意味はありません。計算する関数f(x)によって変える必要があります。
039 040
// ニュートン法で計算
x = newtons( x_ans, a );
ニュートン法の漸化式にx_ansとaを渡して、次のxの値を取得しています。
042 043 044
// 収束の判定 if ( e > Math.abs( x - x_ans ) ) return Math.abs( x );
046 047
// 最新の計算結果を次の計算結果に代入
x_ans = x;
x_ansにxを代入しています。この後、計算は続きます。
050 051
// 収束しなかった場合、マイナスの値を戻す return -1.0;
055 056
// メイン public static void main(String[] args) {
060 061
// 平方根を求める値を代入
a = 77.7 * 77.7;
063 064
// 結果の表示 System.out.println( a + "の平方根: " + sqrt( a ) );
以上です。
ニュートン法に関するコンテンツ
「ニュートン法」に関係があるコンテンツをまとめています。


