2020/03/23 公開

・ピタゴラスの定理

ピタゴラスの定理（三平方の定理）は、直角三角形の三辺の長さの関係を表すもので、斜辺の長さをc、他の２つの辺の長さをa、bとするとき

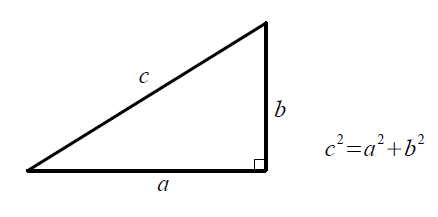
という式が成り立ちます。これがピタゴラスの定理の公式です。

次に、なぜこの式が成り立つかを説明していきます。

下の図は、１辺の長さが( a + b )の正方形の中に、１辺の長さがcの正方形が内接して状態です。。

この外側の正方形の面積は、１辺の長さが( a + b )なので

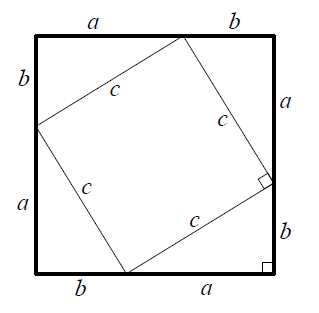
で計算できます。

また、外側の正方形の四隅の三角形の面積(底辺a、高さb)と、内側の１辺の長さがcの正方形の面積を合計した式

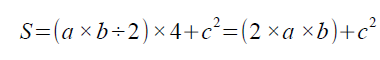
でも計算できます。

上記の２つの式で計算した面積は同じなので以下の式が成り立ちます。

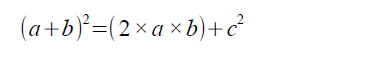
この式の左辺を展開します。

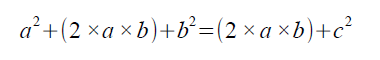
両辺から（2×a×b)を消去すると以下の式になります。

この式は、ピタゴラスの定理の公式と同じです。

ピタゴラスの定理を使った計算例は、こちらを参照してください。「２点間の距離」

■関連コンテンツ

	計算結果の表示 足し算(加法)／引き算(減法)／掛け算(乗法)／割り算(除法)の使い方を説明
	三角形の面積計算 底辺と高さを与えて、三角形の面積を計算する方法を解説します。三角形の面積は、（底辺×高さ）÷２で計算できます。

■新着情報

■広告