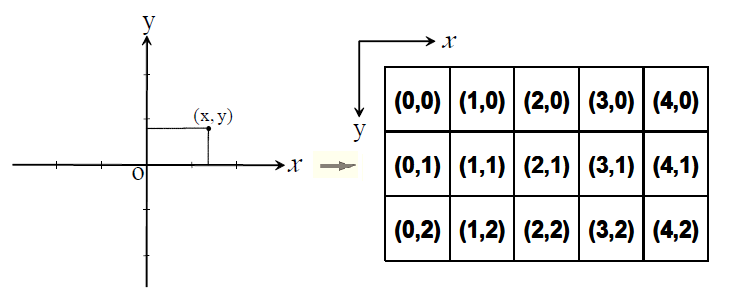
座標変換
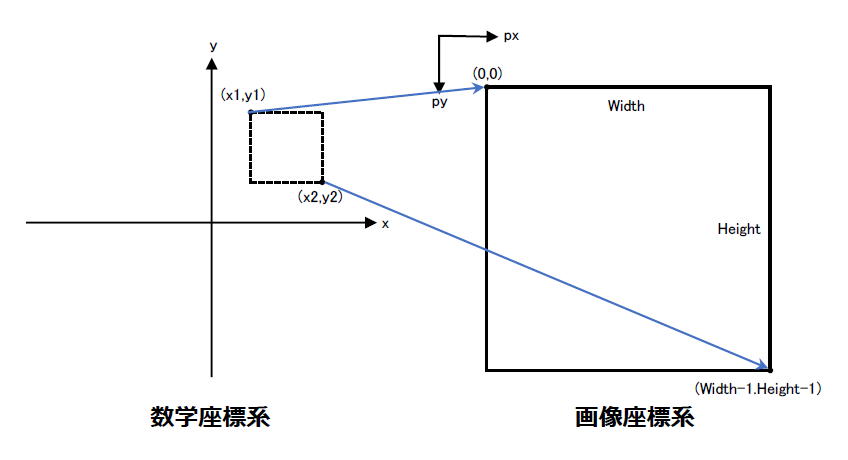
数学xy→画像xy
px = ax + b…式① py = cy + d…式②
a、b、c、dは任意の値で、この値でどのように変換するかを決めます。ちなみに、これらの式では回転はできません。
次に、a、b、c、dの決め方を説明します。
次に、式①に２つの組のx座標を代入します。
px1 = ax1 + b…式③ px2 = ax2 + b…式④
ここから式③と式④からa、bを求めていきます。
式③から式④を引くと、
px1 - px2 = ax1 - ax2 …式⑤
となります。
式⑤の右辺をaでまとめると
px2 - px2 = a( x1 - x2 )…式⑥
となります。
式⑥の両辺を( x1 - x2 )で割るとaが求まります。
a = ( px1 - px2 ) / ( x1 - x2 )
次に、bを求めていきます。
式③の両辺にx2を掛けた式⑦と、式④の両辺にx1を掛けた式⑧を作ります。
px1・x2 = ax1・x2 + bx2…式⑦ px2・x1 = ax2・x1 + bx1…式⑧
式⑦から式⑧を引くと、
px1・x2 - px2・x1 = bx2 - bx1 …式⑨
となります。
式⑨の右辺をbでまとめると
px1・x2 - px2・x1 = b( x2 - x1 ) …式⑩
となります。
式⑲の両辺を( x2 - x1 )で割るとbが求まります。
b = ( px1・x2 - px2・x1 ) / ( x2 - x1 )
同様に、式②に２つの組のy座標を代入します。
py1 = cy1 + d…式⑤ py2 = cy2 + d…式⑥
これをaとbを求めた方法でcとdを求めると、
c = ( py1 - py2 ) / ( y1 - y2 ) d = ( py1・y2 - py2・y1 ) / ( y2 - y1 )
となります。
まとめると、
a = ( px1 - px2 ) / ( x1 - x2 ) b = ( px1・x2 - px2・x1 ) / ( x2 - x1 ) c = ( py1 - py2 ) / ( y1 - y2 ) d = ( py1・y2 - py2・y1 ) / ( y2 - y1 )
です。
Javaソースコード
Transformation2d.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045
public class Transformation2d { // 変換パラメータ a,b,c,d private double a = 0.0; private double b = 0.0; private double c = 0.0; private double d = 0.0; // パラメータを計算 boolean set( double x1, double y1, double x2, double y2, double px1, double py1, double px2, double py2 ) { // ゼロとみなす値 double e = 0.0000000001; // 初期値を代入 a = b = c = d = 0.0; // x1とx2が同じ値であればエラー if ( e > Math.abs( x1 - x2 ) ) return false; // y1とy2が同じ値であればエラー if ( e > Math.abs( y1 - y2 ) ) return false; // パラメータの計算 a = ( px1 - px2 ) / ( x1 - x2 ); b = ( px1 * x2 - px2 * x1 ) / ( x2 - x1 ); c = ( py1 - py2 ) / ( y1 - y2 ); d = ( py1 * y2 - py2 * y1 ) / ( y2 - y1 ); return true; } // 変換後のx座標を取得 public double getX( double x ) { return a * x + b; } // 変換後のy座標を取得 public double getY( double y ) { return c * y + d; } }
ここから、メソッドについて簡単に説明していきます。
008 009 010
// パラメータを計算 boolean set( double x1, double y1, double x2, double y2, double px1, double py1, double px2, double py2 )
数学座標の範囲(x1,y1)-(x2,y2)と変換後の画像座標の範囲(px1,py1)-(px2,py2)を与えて変換パラメータを設定するメソッドです。x1とx2が同じ値、またはy1とy2が同じ値の場合、エラーとなります。
034 035
// 変換後のx座標を取得 public double getX( double x )
040 041
// 変換後のy座標を取得 public double getY( double y )
以上です。
関連コンテンツ
広告
