2020/3/23
2025/3/06
単位ベクトル
はじめに
単位ベクトルとは、長さ（ノルム）が１のベクトルのことです。下の図のように方向に関係なく、長さが１であれば単位ベクトルです。長さが1でないベクトルは単位ベクトルではありません。
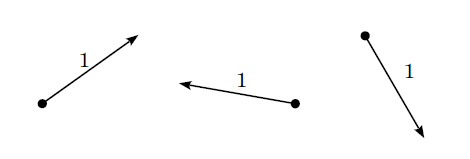単位ベクトルの例
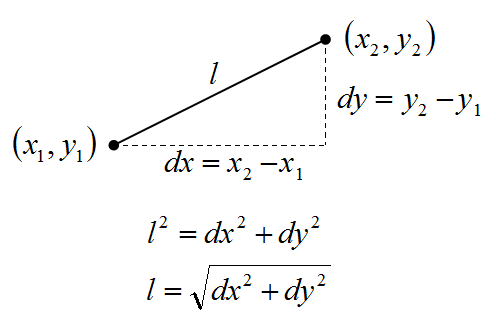
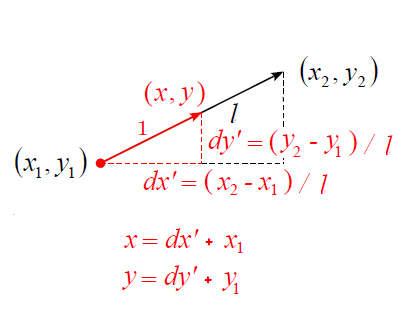
与えられた２つの座標(x1,y1)と(x2,y2)の距離lをピタゴラスの定理によって計算し、その距離lでx成分の差dxとy成分の差dyを割りdx'とdy'を求めます。dx'とdy'のそれぞれに(x1,y1)を足して(x,y)を求めます。
Javaソースコード
UnitVector.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053
public class UnitVector { public static void main( String[] args ) { double x1, y1; double x2, y2; double l; double dx, dy; double x, y; // １つ目の座標を代入 x1 = 60.0; y1 = 20.0; // ２つ目の座標を代入 x2 = 10.0; y2 = 40.0; // x座標の差を計算してdxに代入 dx = x2 - x1; // y座標の差を計算してdyに代入 dy = y2 - y1; // ２点間の距離を計算してlに代入 l = Math.sqrt( dx * dx + dy * dy ); // (x1,y1)から距離1の座標(x,y)を計算 x = dx / l + x1; y = dy / l + y1; // 結果を表示 System.out.println( "x=" + x ); System.out.println( "y=" + y ); System.out.println( "距離=" + dist( x1, y1, x, y ) ); } // (x1,y1)-(x2,y2)の直線距離を計算するメソッド private static double dist( double x1, double y1, double x2, double y2 ) { double l; double dx, dy; // x座標の差を計算してdxに代入 dx = x2 - x1; // y座標の差を計算してdyに代入 dy = y2 - y1; // ２点間の距離を計算してlに代入 l = Math.sqrt( dx * dx + dy * dy ); // 計算した距離を返す return l; } }
実行結果
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis UnitVector.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac UnitVector.java
実行
C:\talavax\javasample>java UnitVector
出力結果
x=59.07152330911474 y=20.371390676354103 距離=1.000000000000002
Javaソースコード解説
ここから、単位ベクトルの成分(x,y)を計算している箇所の説明をしていきます。
017 018 019 020
// x座標の差を計算してdxに代入 dx = x2 - x1; // y座標の差を計算してdyに代入 dy = y2 - y1;
022 023
// ２点間の距離を計算してlに代入
l = Math.sqrt( dx * dx + dy * dy );
025 026 027
// (x1,y1)から距離1の座標(x,y)を計算
x = dx / l + x1;
y = dy / l + y1;
dxとdyをそれぞれlで割って、単位ベクトルの成分xとyを求めています。このソースでは、lが0.0の場合にdxとdyを割らないように制御していません。dxとdyを0で割ると計算値がInfinity(無限大）になります。
029 030 031 032
// 結果を表示 System.out.println( "x=" + x ); System.out.println( "y=" + y ); System.out.println( "距離=" + dist( x1, y1, x, y ) );
以上です。
関連コンテンツ
広告
