数学関数逆三角関数 atan3 - 【ゆるゆるプログラミング】

2016.02.21

逆三角関数 atan3

はじめに

ここでは、xとyを引数として渡し、x軸からの反時計周り（左周り）の角度 θ（ラジアン）を0～2πの値で戻すメソッドの作り方を説明します。

下図は、xとyとθの関係を表したものです。

$atan2$

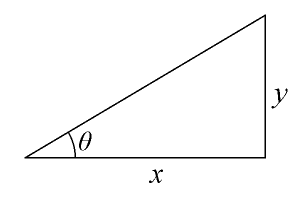
メソッドの作り方

それでは、作り方を説明します。

Javaには、既にxとyからθを求めるMath.atan2メソッドが有ります。このメソッドは、yが0以上のときθを0～π、yが0未満のときθを－π～0の値を戻します。

yが0以上の場合は、Math.atan2の戻り値はx軸からの反時計周りの角度なのでそのまま使います。yが0未満の場合、戻り値の角度が－π～0となるので、この値を反時計周りの角度に変換します。変換方法は簡単で、戻り値に2πを足すだけです。

Javaソースコード

以下のJava ソースコードのatan3メソッドが、xとyを引数として渡し、x軸からの反時計周り（左周り）の角度 θ（ラジアン）を0～2πの値で戻すメソッドです。

Atan3Sample.java

ダウンロード

public class Atan3Sample {
	// Math.atan2メソッドを利用し、角度の戻り値を0～2πにしたもの
	private static double atan3( double y, double x )
	{
		// yが0以上の場合
		if ( 0.0 <= y )
			return Math.atan2( y, x );

		// yが0未満の場合
		return Math.atan2( y, x ) + 2.0 * Math.PI;
	}


	// メイン
	public static void main(String[] args) {
		// 右 0°(x軸上)
		System.out.println( "x= 1, y= 0 : atan3=" + atan3(  0.0,  1.0 ) );

		// 右上 45°
		System.out.println( "x= 1, y= 1 : atan3=" + atan3(  1.0,  1.0 ) );

		// 上 90°(y軸上)
		System.out.println( "x= 0, y= 1 : atan3=" + atan3(  1.0,  0.0 ) );

		// 左上 135°
		System.out.println( "x=-1, y= 1 : atan3=" + atan3(  1.0, -1.0 ) );

		// 右 180°(x軸上)
		System.out.println( "x=-1, y= 0 : atan3=" + atan3(  0.0, -1.0 ) );

		// 左下 225°
		System.out.println( "x=-1, y=-1 : atan3=" + atan3( -1.0, -1.0 ) );

		// 下 270°(y軸上)
		System.out.println( "x= 0, y=-1 : atan3=" + atan3( -1.0,  0.0 ) );

		// 右下 315°
		System.out.println( "x= 1, y=-1 : atan3=" + atan3( -1.0,  1.0 ) );

		// 原点(0,0)
		System.out.println( "x= 0, y= 0 : atan3=" + atan3(  0.0,  0.0 ) );
	}
}

コンパイルソースコードが「ANSI」の場合

C:\talavax\javasample>javac -encoding sjis Atan3Sample.java

コンパイルソースコードが「UTF-8」の場合

C:\talavax\javasample>javac Atan3Sample.java

実行

C:\talavax\javasample>java Atan3Sample

x軸上、y軸上、第１～４象限、原点座標の(x,y)に対して、atan3メソッドの結果を表示しています。

出力結果

x= 1, y= 0 : atan3=0.0
x= 1, y= 1 : atan3=0.7853981633974483
x= 0, y= 1 : atan3=1.5707963267948966
x=-1, y= 1 : atan3=2.356194490192345
x=-1, y= 0 : atan3=3.141592653589793
x=-1, y=-1 : atan3=3.9269908169872414
x= 0, y=-1 : atan3=4.71238898038469
x= 1, y=-1 : atan3=5.497787143782138
x= 0, y= 0 : atan3=0.0

x軸を基準に反時計周り（左周り）の角度（ラジアン）の値を返していることが確認できます。

以上です。