2016.01.07
2025.03.05
逆三角関数 逆余弦 acos

はじめに
cosθ → θは?
メソッド
Math.acosメソッド
public static double Math.acos( double a )
・引数aで指定した値の逆余弦 (アークコサイン)を返します。 パラメータ a : 余弦 (コサイン)の値。 戻り値 aの逆余弦 (アークコサイン)をラジアンで戻す。
メソッド使用時に注意すること
このメソッドを使うときに注意することを書いておきます。
1つ目は、渡す引数の範囲は-1.0~1.0であるということです。範囲外の値を引数として渡すとメソッドはNaNを戻します。
2つ目は、戻り値の角度(ラジアン)の範囲は0.0~πであるということです(πはパイ)。ある角度θをMath.cosメソッドに代入して得られた値を、Math.acosメソッドに代入するとθ'が得られたとします。その結果は、必ずしもθ=θ'となりません。それは、同じ値のcosを示す角度は、0~2π(360°)の中に1または2つあるからです。cosθ=1のときθ=0(0°)、cosθ=-1のときθ=π(180°)となり、θを1つだけ求めることが出来ますが、それ以外のときはθの候補が2つ存在します。Math.acosのメソッド戻り値の範囲を0.0~πとすることでθの候補を1つに絞っています。
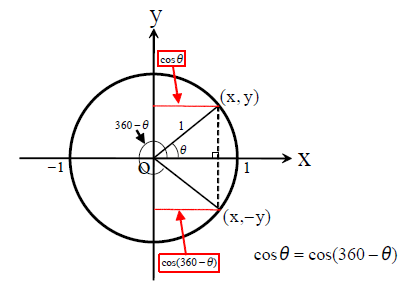
以下の図は、cosθとcos(360°-θ)が同じになることを示している図で、cosに渡す角度が違ってもcosの値が同じになることが分かります。
以上です。Math.acosメソッドを使うときの参考にしてください。
Javaソースコード
Math.acosメソッドを使ったJavaソースコードを紹介します。
AcosSample.java
001 002 003 004 005 006 007 008 009 010 011 012
public class AcosSample { public static void main( String[] args ) { // 30°をラジアンに変換 double rad1 = Math.toRadians( 30.0 ); // 330°をラジアンに変換 double rad2 = Math.toRadians( 360.0 - 30.0 ); // 結果の表示 System.out.println( Math.acos( Math.cos( rad1 ) ) ); System.out.println( Math.acos( Math.cos( rad2 ) ) ); } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis AcosSample.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac AcosSample.java
実行
C:\talavax\javasample>java AcosSample
実行結果
0.5235987755982987 0.5235987755982994
出力された2つ値は、30°をラジアンに変換した値とほぼ一致しています。
Javaソースコードの解説
ここからは、このソースコードを上から順番に解説していきます。
001
public class AcosSample {
クラス名を、AcosSampleとしています。
002
public static void main( String[] args ) {
003 004
// 30°をラジアンに変換 double rad1 = Math.toRadians( 30.0 );
30°をMath.toRadiansメソッドでラジアンに変換し、変数rad1に代入しています。
005 006
// 330°をラジアンに変換 double rad2 = Math.toRadians( 360.0 - 30.0 );
150°をMath.toRadiansメソッドでラジアンに変換し、変数rad2に代入しています。
Math.toRadiansメソッド
public static double Math.toRadians( double a )
・引数aで指定した角度をラジアンに変換した値を返します。 パラメータ a : 角度(単位:度)[ 戻り値 ラジアン
008 009
// 結果の表示
System.out.println( Math.acos( Math.cos( rad1 ) ) );
Math.cosメソッドにrad1を渡して求めたcosの値を、Math.acosメソッドに渡した結果をコンソール出力しています。
010
System.out.println( Math.acos( Math.cos( rad2 ) ) );
Math.cosメソッドにrad2を渡して求めたcosの値を、Math.acosメソッドに渡した結果をコンソール出力しています。
Math.cosメソッド
public static double Math.cos( double a )
・引数aで指定した角度の余弦 (コサイン) を返します。 パラメータ a : ラジアンで指定した角度。 戻り値 aの余弦
以上です。
逆三角関数に関するコンテンツ
「逆三角関数」に関係があるコンテンツをまとめています。