2019.06.21
2025.03.11
円周率πを計算で求める その1
はじめに
円の面積は、
(半径×半径×円周率π)
(1×1×円周率π)=円周率π
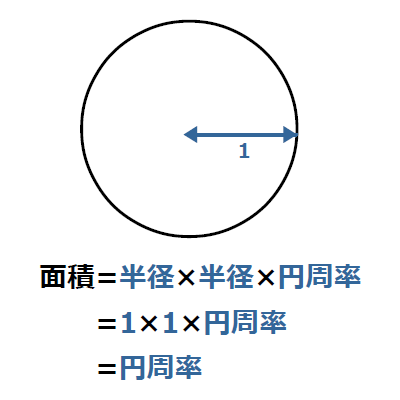
ここからは、単位円の面積を計算する方法を説明していきます。
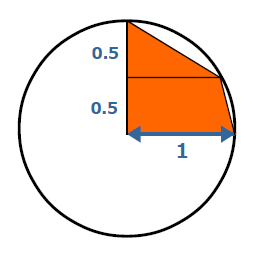
単位円の右上1/4を台形(一番上は三角形)に分割します。このとき台形の高さを全て同じにします。
下図の例は、単位円の右上1/4を2つの台形に分割した例です。
オレンジ色で塗りつぶされている部分が台形の範囲です。2つの台形に分割しているので、それぞれの台形の高さは0.5です。
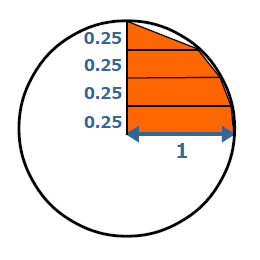
以下の例は、単位円の右上1/4を4つの台形に分割した例です。
4つの台形に分割しているので、それぞれの台形の高さは1を4で割った0.25になります。
Javaソースコード
以下は、円周率πを計算するJavaソースコードです。
CalcPI1.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071 072
public class CalcPI1 { // πを計算するメソッド public static double getPI_1( int yn ) { double upperbase; // 台形の上底 double lowerbase; // 台形の下底 double height; // 台形の高さ double lowery; // 台形の下底の座標 double area; // 円の面積 double aread; // 台形の面積 // 台形の高さ(円の半径をynで割る) height = 1.0 / (double)yn; // 上底の初期値 upperbase = 0.0; // 下底のy座標の初期値 lowery = 1.0 - height; // 計算開始 area = 0.0; for ( int i = 0; i < yn; ++ i ) { // 下底の計算 lowerbase = Math.sqrt( 1.0 - lowery * lowery ); // 台形の面積計算 aread = ( upperbase + lowerbase ) * height / 2.0; // 円の面積に台形の面積を足す area += aread; // 下底を上底に代入 upperbase = lowerbase; // 下底のy座標からheightを引く lowery -= height; } // 1/4円の面積を4倍 area = area * 4.0; // 結果を戻す return area; } public static void main( String[] args ) { // yの分割数 int yn; // 1000分割 yn = 1000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); // 10000分割 yn = 10000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); // 100000分割 yn = 100000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); // 1000000分割 yn = 1000000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); // 10000000分割 yn = 10000000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis CalcPI1.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac CalcPI1.java
実行
C:\talavax\javasample>java CalcPI1
出力結果
分割数:1000 π=3.1415554669110293 分割数:10000 π=3.1415914776112435 分割数:100000 π=3.141592616398606 分割数:1000000 π=3.1415926524339723 分割数:10000000 π=3.1415926531488605
3.141592653589793238462・・・
です。分割数を1000000にすると小数点以下第9桁まで一致しました。
Javaソースコードの解説
001
public class CalcPI1 {
クラス名を、CalcPI1としています。
002 003
// πを計算するメソッド public static double getPI_1( int yn )
005 006 007 008 009 010
double upperbase; // 台形の上底 double lowerbase; // 台形の下底 double height; // 台形の高さ double lowery; // 台形の下底の座標 double area; // 円の面積 double aread; // 台形の面積
計算に使用する変数を宣言しています。
012 013
// 台形の高さ(円の半径をynで割る) height = 1.0 / (double)yn;
015 016
// 上底の初期値
upperbase = 0.0;
018 019
// 下底のy座標の初期値
lowery = 1.0 - height;
021 022 023
// 計算開始 area = 0.0; for ( int i = 0; i < yn; ++ i ) {
024 025
// 下底の計算
lowerbase = Math.sqrt( 1.0 - lowery * lowery );
027 028
// 台形の面積計算
aread = ( upperbase + lowerbase ) * height / 2.0;
030 031
// 円の面積に台形の面積を足す
area += aread;
033 034
// 下底を上底に代入
upperbase = lowerbase;
036 037
// 下底のy座標からheightを引く
lowery -= height;
040 041
// 1/4円の面積を4倍
area = area * 4.0;
043 044
// 結果を戻す return area;
048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068 069 070 071
public static void main( String[] args ) { // yの分割数 int yn; // 1000分割 yn = 1000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); // 10000分割 yn = 10000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); // 100000分割 yn = 100000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); // 1000000分割 yn = 1000000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); // 10000000分割 yn = 10000000; System.out.println( "分割数:" + yn+ " π=" + getPI_1( yn ) ); }
以上です。
円周率πに関するコンテンツ
- 円の直径と半径
- 有限小数と無限小数
- 点が円内かを判定
- 球の表面積/体積計算
- 円の面積計算
- 立方体の表面積/体積計算
- 数学関数 三角関数 cos
- 格子座標から円周率πを計算
- 円周率πを計算で求める その2
- 数学定数 円周率π(パイ)
- 角度とラジアンの相互変換
- 数学関数 三角関数 sin
- 数学関数 三角関数 tan
- tan(タンジェント)
- 円周上のランダムな座標を求める その1
- 円周上のランダムな座標を求める その2
- 円周上のランダムな座標を求める その3
- 単位円
- 変数について
- 円弧の長さ
- マルウェア
- 数学関数 逆三角関数 acos
- 数学関数 逆三角関数 asin
- 数学関数 逆三角関数 atan
- 数学関数 逆三角関数 atan2
- 数学関数 逆三角関数 atan3
- メソッド
- 放射状模様
- プログラミング言語
- 実数と虚数
- キーボード入力した角度のsin、cosを計算
- 表面積


