2020.3.23
2025.1.23
数学定数 円周率π(パイ)
円周率π(パイ)とは
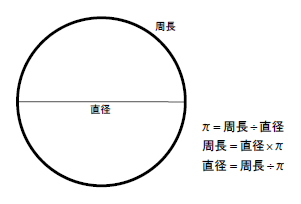
Math.PI定数
public static double Math.PI
・円周率πの値 3.141592...
以上です。
円周率に関するコンテンツ
「円周率」に関係があるコンテンツをまとめています。
- 円の直径と半径
- 有限小数と無限小数
- 点が円内かを判定
- 球の表面積/体積計算
- 円の面積計算
- 立方体の表面積/体積計算
- 円周率πを計算で求める その1
- 数学関数 三角関数 cos
- 格子座標から円周率πを計算
- 円周率πを計算で求める その2
- 角度とラジアンの相互変換
- 数学関数 三角関数 sin
- 数学関数 三角関数 tan
- tan(タンジェント)
- 円周上のランダムな座標を求める その1
- 円周上のランダムな座標を求める その2
- 円周上のランダムな座標を求める その3
- 単位円
- 変数について
- 円弧の長さ
- マルウェア
- 数学関数 逆三角関数 acos
- 数学関数 逆三角関数 asin
- 数学関数 逆三角関数 atan
- 数学関数 逆三角関数 atan2
- 数学関数 逆三角関数 atan3
- メソッド
- 放射状模様
- プログラミング言語
- 実数と虚数
- キーボード入力した角度のsin、cosを計算
- 表面積
円周率π関連のプログラム(作ってみました)
円周率π関連のプログラム(作ってみました)- 計算結果が精度が悪い方法
円の中に含まれる格子の数と格子の外の数から円周率πを計算する方法を紹介しています。図とJavaのソースコードでくわしく説明していますので、興味のある方は記事をご覧ください。
2020.12.22
関連コンテンツ
円の中に含まれる格子の数と格子の外の数から円周率πを計算する方法を紹介しています。図とJavaのソースコードでくわしく説明していますので、興味のある方は記事をご覧ください。
2020.12.22
円の中心座標(0,0)、半径rで表される円の円周上のランダムな座標を求めるJavaのソースコードを紹介しています。ラジアンを乱数で発生して座標を計算しています。
2022.09.27



