数学関数逆三角関数 atan2 - 【ゆるゆるプログラミング】

2016.02.21

逆三角関数 atan2

はじめに

atan2(アークタンジェント、逆正接)は、座標(0,0)とメソッドの引数(x,y)を結んだ直線とx軸の角度 θ（ラジアン）を求めるものです。

xとyと角度 θの関係を図にすると以下のようになります。

$アークタンジェント$

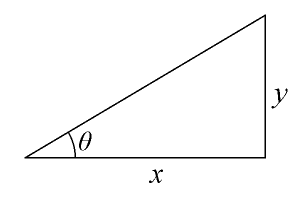
アークタンジェント

Math.atan2メソッドにxとｙを渡すとθが戻ります。y、xの順番で引数に渡す仕様になっています。注意して使用してください。

Math.atan2メソッド

public static double Math.atan2(double y, double x )

・引数x,yで指定した値の逆正接 (アークタンジェント)を返します。

  パラメータ y : y座標の値。
  　　　　　 x : x座標の値。

  戻り値     y/xの逆正接（アークタンジェント）をラジアンで戻す。

角度は、yが0以上の場合、x軸を基準に反時計周り（左周り）で求められ、戻り値の角度（ラジアン）の範囲は0以上、π以下です（πはパイ）。yの値が0以上の範囲は、下図の水色で表しています。

$atan2$

yが0未満の場合、角度はx軸を基準に時計周り（右周り）で求められ、戻り値の角度（ラジアン）の範囲は-πより大きい、0未満です（πはパイ）。yの値が0未満の範囲は、下図の水色で表しています。

$atan2$

ちなみに、x=0、y=0を引数として渡すと0が戻ります。実際には(0,0)の角度は不定ですが、JavaのMath.atan2は0を戻します。

Javaソースコード

Math.atan2メソッドを使ったJava ソースコードを紹介します。

Atan2Sample.java

ダウンロード

public class Atan2Sample {
	public static void main(String[] args) {
		// 右 0°(x軸上)
		System.out.println( "x= 1, y= 0 : atan2=" + Math.atan2(  0.0,  1.0 ) );

		// 右上 45°
		System.out.println( "x= 1, y= 1 : atan2=" + Math.atan2(  1.0,  1.0 ) );

		// 上 90°(y軸上)
		System.out.println( "x= 0, y= 1 : atan2=" + Math.atan2(  1.0,  0.0 ) );

		// 左上 135°
		System.out.println( "x=-1, y= 1 : atan2=" + Math.atan2(  1.0, -1.0 ) );

		// 右 180°(x軸上)
		System.out.println( "x=-1, y= 0 : atan2=" + Math.atan2(  0.0, -1.0 ) );

		// 左下 225°
		System.out.println( "x=-1, y=-1 : atan2=" + Math.atan2( -1.0, -1.0 ) );

		// 下 270°(y軸上)
		System.out.println( "x= 0, y=-1 : atan2=" + Math.atan2( -1.0,  0.0 ) );

		// 右下 315°
		System.out.println( "x= 1, y=-1 : atan2=" + Math.atan2( -1.0,  1.0 ) );

		// 原点(0,0)
		System.out.println( "x= 0, y= 0 : atan2=" + Math.atan2(  0.0,  0.0 ) );
	}
}

コンパイルソースコードが「ANSI」の場合

C:\talavax\javasample>javac -encoding sjis Atan2Sample.java

コンパイルソースコードが「UTF-8」の場合

C:\talavax\javasample>javac Atan2Sample.java

実行

C:\talavax\javasample>java Atan2Sample

x軸上、y軸上、第１～４象限、原点座標の(x,y)に対して、atan2メソッドの結果を表示しています。

実行結果

x= 1, y= 0 : atan2=0.0
x= 1, y= 1 : atan2=0.7853981633974483
x= 0, y= 1 : atan2=1.5707963267948966
x=-1, y= 1 : atan2=2.356194490192345
x=-1, y= 0 : atan2=3.141592653589793
x=-1, y=-1 : atan2=-2.356194490192345
x= 0, y=-1 : atan2=-1.5707963267948966
x= 1, y=-1 : atan2=-0.7853981633974483
x= 0, y= 0 : atan2=0.0

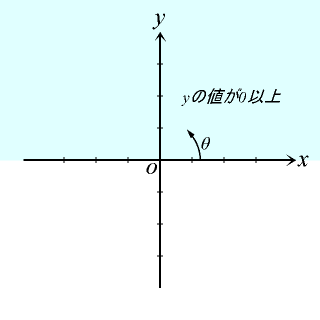
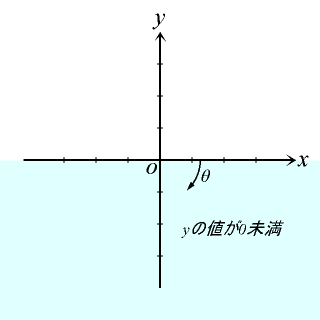
yが0以上の場合、0からπの値を返していることが分かります。yが0未満の場合、-0から-πの値を返していることが分かります。0からπの値を返していることが分かります。また、x=0、y=0の場合、0.0を返していることが確認できます。

以上です。