2020/3/23
2025/1/21
単位円
単位円とは
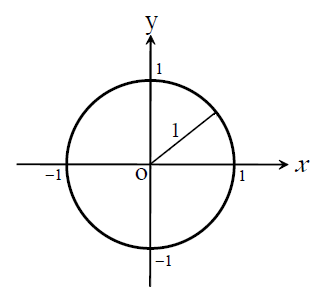
単位円
単位円の円周
円周は、以下の式で計算することができます。
円周 = π×直径 円周 = 2π × 半径
円周 = 2π × 半径 = 2π × 1 = 2π
となります。
2πが単位円の円周です。
単位円の面積
円の面積は、以下の式で計算することができます。
円の面積 = π× 半径2
円の面積 = π× 12 = π× 1 = π
となります。
πが単位円の面積です。
単位円と三角関数の関係
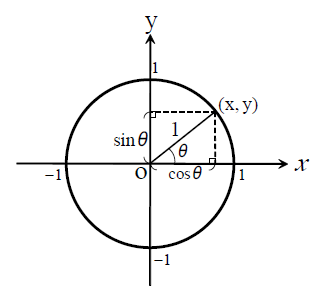
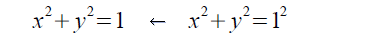
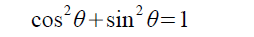
これらの式は、ピタゴラスの定理から簡単に導き出せます。
以上です。
単位円に関するコンテンツ
「単位円」に関係があるコンテンツをまとめています。
関連コンテンツ
円の中に含まれる格子の数と格子の外の数から円周率πを計算する方法を紹介しています。図とJavaのソースコードでくわしく説明していますので、興味のある方は記事をご覧ください。
2020.12.22