2020.12.22
数学
格子座標から円周率πを計算
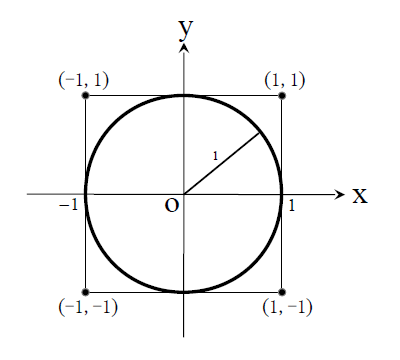
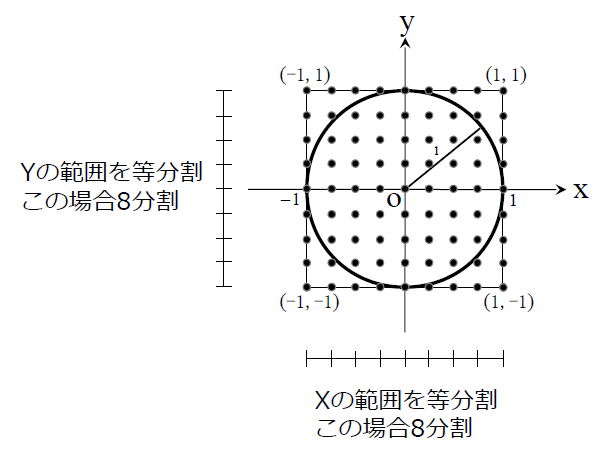
よって、以下の比が成り立ちます。
となります。
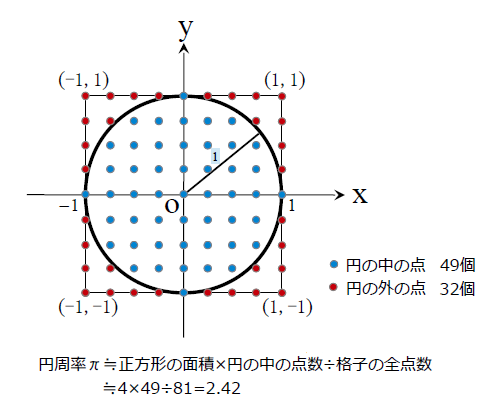
Javaソースコード
GridPI.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067
public class GridPI { public static void main( String[] args ) { // 変数の宣言 int cellnum; int x, y; double in_num; double left, right; double top, bottom; double celllen; double cellx, celly; double l2; // 単位円に外接する正方形の左上と右下の座標を代入 // 左上の座標 left = -1.0; top = 1.0; // 右下の座標 right = 1.0; bottom = -1.0; // １辺の格子の数 cellnum = 20000; // セルの幅を計算(x軸だけで計算) celllen = ( right - left ) / (double)( cellnum - 1 ); // 円周率πの計算のメイン // 円内の座標の個数を初期化 in_num = 0.0; // 格子のy座標の初期値 celly = top; for ( y = 0; y < cellnum; y++ ) { // 格子のx座標の初期値 cellx = left; for ( x = 0; x < cellnum; x++ ) { // 単位円の中心座標(0,0)と //セルの直線距離の２乗を計算 l2 = cellx * cellx + celly * celly; // 単位円の中かを判定 if ( 1.0 >= l2 ) { // 単位円の中と判定 // 単位円の線上も中と判定 ++ in_num; } // 格子のx座標にセルの幅を足す cellx += celllen; } // 格子のy座標からセルの幅を引く celly -= celllen; } // 外接正方形の面積を計算(計算結果は4.0) double sq_area = ( right - left ) * ( top - bottom ); // 格子全体の座標数 double all_num = (double)cellnum * (double)cellnum; // 円周率πを計算 double pi = sq_area * in_num / all_num; // 結果を出力 System.out.println( pi ); } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis GridPI.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac GridPI.java
実行
C:\talavax\javasample>java GridPI
出力結果
3.14127716
３．１４１５９２６５３５８９７９３２３８４６２・・・
です。分割数20000でも小数点以下第３桁までしか一致しません。
この方法は、精度は悪く実用的ではないです。
Javaソースコードの解説
001
public class GridPI {
クラス名を、GridPIとしています。
002
public static void main( String[] args ) {
003 004 005 006 007 008 009 010 011
// 変数の宣言 int cellnum; int x, y; double in_num; double left, right; double top, bottom; double celllen; double cellx, celly; double l2;
013 014 015 016
// 単位円に外接する正方形の左上と右下の座標を代入 // 左上の座標 left = -1.0; top = 1.0;
018 019 020
// 右下の座標
right = 1.0;
bottom = -1.0;
022 023
// １辺の格子の数
cellnum = 20000;
025 026
// セルの幅を計算(x軸だけで計算) celllen = ( right - left ) / (double)( cellnum - 1 );
028 029 030
// 円周率πの計算のメイン // 円内の座標の個数を初期化 in_num = 0.0;
032 033 034 035 036 037
// 格子のy座標の初期値 celly = top; for ( y = 0; y < cellnum; y++ ) { // 格子のx座標の初期値 cellx = left; for ( x = 0; x < cellnum; x++ ) {
038 039 040 041 042 043 044 045 046 047
// 単位円の中心座標(0,0)と //セルの直線距離の２乗を計算 l2 = cellx * cellx + celly * celly; // 単位円の中かを判定 if ( 1.0 >= l2 ) { // 単位円の中と判定 // 単位円の線上も中と判定 ++ in_num; }
単位円の中心座標(0,0)と(cellx,celly)の直線距離の２乗を計算した値を変数l2に代入し、その値が単位円の半径の２乗(1.0=1.0x1.0)以下の場合に円の中に入っていると判定し、変数in_numに１を足しています。
048 049 050 051 052
// 格子のx座標にセルの幅を足す cellx += celllen; } // 格子のy座標からセルの幅を引く celly -= celllen;
変数xのfor文でcellxにcelllenを足しています。変数yのfor文でcellyからcelllenを引いています。
これで左上から右下の順番で格子座標(cellx,celly)を求めています。
055 056
// 外接正方形の面積を計算(計算結果は4.0) double sq_area = ( right - left ) * ( top - bottom );
058 059
// 格子全体の座標数 double all_num = (double)cellnum * (double)cellnum;
061 062
// 円周率πを計算 double pi = sq_area * in_num / all_num;
064 065
// 結果を出力
System.out.println( pi );
以上です。
関連コンテンツ
広告
