2019.05.23
2025.03.18
ニュートン法で平方根 その2
はじめに
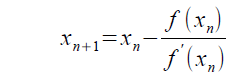
ニュートン法の式の中にf(x)をxで微分したf'(x)を含んでいますが、関数f(x)によってf'(x)を導くことが困難または不可能なことがあります。
関数をf(x)=x2-aとし、f(x)=0となるxを求めることで、aの平方根を計算します。
この式は、以下の手順で導いています。
Javaソースコード
以下がそのJavaソースコードです。
NewtonsMethod2.java
001 002 003 004 005 006 007 008 009 010 011 012 013 014 015 016 017 018 019 020 021 022 023 024 025 026 027 028 029 030 031 032 033 034 035 036 037 038 039 040 041 042 043 044 045 046 047 048 049 050 051 052 053 054 055 056 057 058 059 060 061 062 063 064 065 066 067 068
public class NewtonsMethod2 { // f(x)=x^2-a static double f( double x, double a ) { return x * x - a; } // f(x)の微分f'(x) - 接線の傾き // 微分の式が分からない場合、微分の近似値を計算 static double df_ex( double x, double a ) { double h = 0.0000001; return ( f( x + h, a ) - f( x, a ) ) / h; } // ニュートン法 漸化式 static double newtons( double x, double a ) { return x - f( x, a ) / df_ex( x, a ); } // メイン public static void main(String[] args) { // 変数の宣言 double e = 0.000001; // 収束の判定値 double x; // 計算値を格納 double x_ans; // 1つ前の計算値 double a; // 平行根を求める値 // 平行根を求める値 a = 169.0; // 13×13 // 初期値を代入 x_ans = 10000.0; // 無限ループ for ( int i = 1; ; ++ i ) { // ニュートン法で計算 x = newtons( x_ans, a ); // 収束の判定 if ( e > Math.abs( x - x_ans ) ) break; // 最新の計算結果を次の計算結果に代入 x_ans = x; // 途中経過の表示 System.out.println( "回数:" + i + " 計算結果: " + x_ans ); } // 改行 System.out.println(); // 結果の表示 System.out.println( "計算結果: " + x_ans ); // 結果の絶対値 x_ans = Math.abs( x_ans ); System.out.println( a + "の絶対値: " + x_ans ); // f(x)=0になるかを確認 System.out.println( "f(" + x_ans + ")=" + f( x_ans, a ) ); } }
コンパイル ソースコードが「ANSI」の場合
C:\talavax\javasample>javac -encoding sjis NewtonsMethod2.java
コンパイル ソースコードが「UTF-8」の場合
C:\talavax\javasample>javac NewtonsMethod2.java
実行
C:\talavax\javasample>java NewtonsMethod2
出力結果
回数:1 計算結果: 5000.055835163439 回数:2 計算結果: 2500.0405926789967 回数:3 計算結果: 1250.05263083155 回数:4 計算結果: 625.0944750620009 回数:5 計算結果: 312.682233554483 回数:6 計算結果: 156.6113993198339 回数:7 計算結果: 78.84524510893075 回数:8 計算結果: 40.494340546011806 回数:9 計算結果: 22.333882320006264 回数:10 計算結果: 14.950430379777575 回数:11 計算結果: 13.127226391861301 回数:12 計算結果: 13.000616525291765 回数:13 計算結果: 13.000000014619735 計算結果: 13.000000014619735 169.0の絶対値: 13.000000014619735 f(13.000000014619735)=3.8011310721230984E-7
Javaソースコードの解説
001
public class NewtonsMethod2 {
002 003 004 005 006
// f(x)=x^2-a static double f( double x, double a ) { return x * x - a; }
009 010 011 012 013 014 015 016
// f(x)の微分f'(x) - 接線の傾き // 微分の式が分からない場合、微分の近似値を計算 static double df_ex( double x, double a ) { double h = 0.0000001; return ( f( x + h, a ) - f( x, a ) ) / h; }
f(x)の微分式f'(x)を数値微分で行うメソッドです。xが0.0000001増加したときの、yの増加分を計算しています。f'(x)は(yの増加分/xの増加分)なので、その値をreturn文で戻しています。ここでは、xの増加分を0.0000001としていますが関数f(x)によって変更する必要があります。いろいろな値で試してください。
019 020 021 022 023
// ニュートン法 漸化式 static double newtons( double x, double a ) { return x - f( x, a ) / df_ex( x, a ); }
026 027
// メイン public static void main(String[] args) {
028 029 030 031 032
// 変数の宣言 double e = 0.000001; // 収束の判定値 double x; // 計算値を格納 double x_ans; // 1つ前の計算値 double a; // 平行根を求める値
034 035
// 平行根を求める値 a = 169.0; // 13×13
037 038
// 初期値を代入
x_ans = 10000.0;
計算の初期値に10000.0を代入しています。この値は任意です。
040 041
// 無限ループ for ( int i = 1; ; ++ i ) {
042 043
// ニュートン法で計算
x = newtons( x_ans, a );
ニュートン法の漸化式にx_ansとaを渡して、次のxの値を取得しています。
045 046
// 収束の判定
if ( e > Math.abs( x - x_ans ) ) break;
048 049
// 最新の計算結果を次の計算結果に代入
x_ans = x;
x_ansにxを代入しています。
055 056 057 058 059
// 改行 System.out.println(); // 結果の表示 System.out.println( "計算結果: " + x_ans );
061 062 063
// 結果の絶対値 x_ans = Math.abs( x_ans ); System.out.println( a + "の絶対値: " + x_ans );
計算結果x_ansの絶対値をとった値をコンソールに出力しています。これが、実際に求めたい平方根の値になります。このプログラムの場合、f(x)=x2-169.0を0.0にするxを求めるようにしてるため、xの値が13.0と-13.0の2つの値のどちらでもf(x)=0を満たすことが出来ます。これは初期値によりプラスとマイナスのどちらかの値をとります。例えば初期値を-10000.0にするとx_ans=-13になります。
065 066
// f(x)=0になるかを確認 System.out.println( "f(" + x_ans + ")=" + f( x_ans, a ) );
計算結果x_ansをメソッドfに代入して、その結果が0になっているか確認するための出力です。この例では、結果の表示が指数表記になっていて、数値の後に'E-7'が付いています。これは10の-7乗を意味しています。この結果から求めたx_ansでメソッドfが戻す値は0に近く、x_ansはaの平方根であることが確認できます。
以上です。
ニュートン法に関するコンテンツ
「ニュートン法」に関係があるコンテンツをまとめています。


