2019.05.22
ニュートン法
はじめに
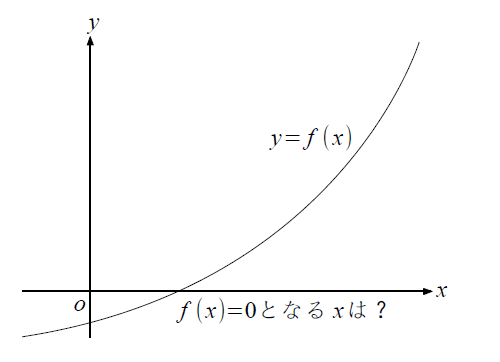
それでは、ニュートン法の考え方を説明します。
はじめに、f(x)=0となるxと予想値x0（任意）を決めて、その値x0でf(x0)の接線を求めます。
次に、接線とx軸の交点の座標(x1,0)を計算し、f(x1)の接線を求めます。
さらに、接線とx軸の交点の座標(x2,0)を計算し、f(x2)の接線を求めます。
以後、接線とx軸の交点を繰り返し計算し、交点のx座標xnの値が変化しなくなれば（収束）、そのx座標xnが求めるxとなります。ただし、関数f(x)=0となるxが存在しない場合は、正しいxは求められません。また、関数f(x)=0となるxが複数存在する場合は、初期値x0の値にって求まるxが変わります。
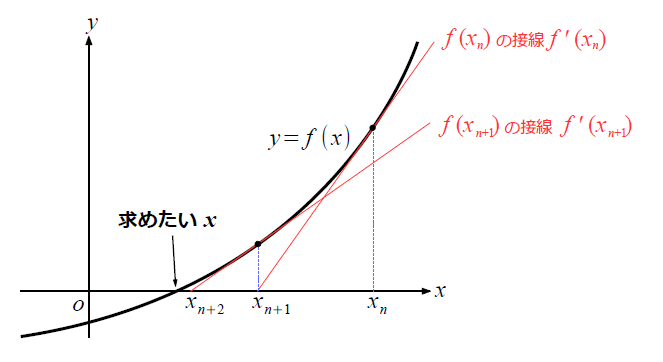
上の図は、接線とx軸の交点を繰り返し計算していく様子を示しています。計算した値が、求めたいxに近づいている様子が確認できます。
f'(x)はf(x)をxで微分したものでf(x)の傾きを表しています。
ここから、ニュートン法を実現するための式について説明していきます。
f(xn)をxnで微分すると、xnの接線の傾きf'(xn)を求めることができます。その傾きf'(xn)をxの増加分⊿x、yの増加分⊿yを使って以下のようにおくと、
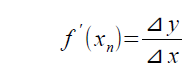
この接線とx軸との交点は、
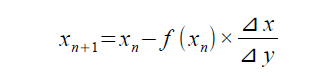
で求められます。（下図）
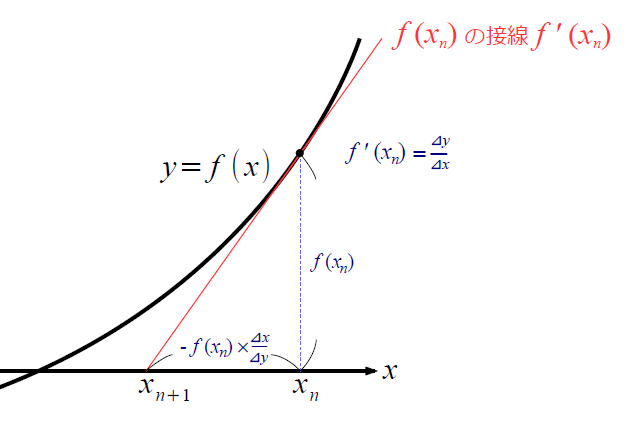
接線の傾きf'(xn)を⊿y／⊿xとおくと、xn+1は、xnからf(xn)×(⊿x／⊿y)を引いた値になります。
最後に、⊿xと⊿yをf'(xn)に置き換えてニュートン法の漸化式にします。
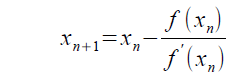
以上です。
関連コンテンツ
広告
