2020/03/23 公開
・２点間の距離
２点間の距離（２次元）とは、２つの座標(x1,y1)と(x2,y2)を結ぶ直線の距離のことです。
下の図は、(x1,y1)と(x2,y2)を結んだ直線と、その距離lを表したものです。
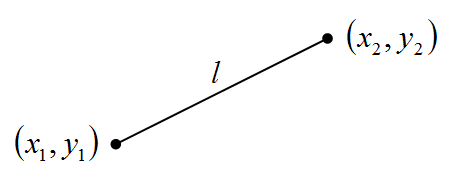２点間の距離
Distance.java ← クリックしてダウンロードページに移動
001: public class Distance {
002: public static void main( String[] args ) {
003: double x1, y1;
004: double x2, y2;
005:
006: // １つ目の座標を代入
007: x1 = 60.0;
008: y1 = 20.0;
009:
010: // ２つ目の座標を代入
011: x2 = 10.0;
012: y2 = 40.0;
013:
014: // 結果を表示
015: System.out.println( dist( x1, y1, x2, y2 ) );
016: }
017:
018:
019: // (x1,y1)-(x2,y2)の直線距離を計算するメソッド
020: private static double dist( double x1, double y1, double x2, double y2 )
021: {
022: double l;
023: double dx, dy;
024:
025: // x座標の差を計算してdxに代入
026: dx = x2 - x1;
027: // y座標の差を計算してdyに代入
028: dy = y2 - y1;
029:
030: // ２点間の距離を計算してlに代入
031: l = Math.sqrt( dx * dx + dy * dy );
032:
033: // 計算した距離を返す
034: return l;
035: }
036: }
Distance.javaの出力結果
53.85164807134504
以下の部分が、２点間の距離を計算するメソッドです。
019: // (x1,y1)-(x2,y2)の直線距離を計算するメソッド
020: private static double dist( double x1, double y1, double x2, double y2 )
021: {
022: double l;
023: double dx, dy;
024:
025: // x座標の差を計算してdxに代入
026: dx = x2 - x1;
027: // y座標の差を計算してdyに代入
028: dy = y2 - y1;
029:
030: // ２点間の距離を計算してlに代入
031: l = Math.sqrt( dx * dx + dy * dy );
032:
033: // 計算した距離を返す
034: return l;
035: }
この計算には、ピタゴラスの定理を使用しています。ピタゴラスの定理は、直角三角形の３辺の長さの関係を表したもので、斜辺の長さの２乗は、他の２つの辺の長さをそれぞれ２乗して値の和（合計）と同じになるというものです。
下の図は、２つの座標間の距離を計算する方法を示した図で、lが２点間の距離で、dxがＸ方向の差を、dyがＹ方向の差を表しています。これをピタゴラスの定理に当てはめると、lが斜辺、dxとdyがその他の２辺です。２点の座標の位置関係によって、２つの辺の長さ（dxとdy）がマイナス(－)の値になることがありますが、これらの値は計算時に２乗するので、結果的に符号が無視され、正しい結果が得られます。
実際に、ソースコードに書かれている数値で、解説していきます。
006: // １つ目の座標を代入 007: x1 = 60.0; 008: y1 = 20.0; 009: 010: // ２つ目の座標を代入 011: x2 = 10.0; 012: y2 = 40.0;
dxは、x2 - x1で計算しているので、dx= 10.0 - 60.0 = -50.0です。dyは、y2-y1で計算しているので、dy=40.0-20.0=20.0です。
２点間の距離lは、dxの２乗とdyの２乗を足した値の平方根なので、dxの２乗= -50.0 x -50.0 = 2500.0と、dyの２乗= 20.0 x 20.0 = 400.0を足した2500.0 + 400.0 = 2900.0の平方根53.85164807134504が、２点間の距離として計算されます。
■関連コンテンツ
| 平方根 | Math.sqrtの使い方について解説 |
| 値の２乗 | 値を２乗するメソッドの作り方を解説 |
| 数学関数について | 数学関数について解説 |
| マンハッタン距離 | マンハッタン距離とは |
| ２点間の距離(３次元) | ２点間の距離計算（３次元） |
| 最も近い座標を探す | １番近い座標は？ |
 |
単位ベクトル単位ベクトルは長さが１のベクトルのことです。任意の長さのベクトルを単位ベクトルに変換する方法も解説しています。 |
 |
単位円単位円は半径が１の円のことです。単位円と三角関数(sinθ、cosθ)の関係についても解説しています。 |
■新着情報
| 2021.06.18 | 変数の初期値 | 変数に値を代入しないで計算 |
| 2021.05.28 | 短針と長針の角度 | 短針と長針の角度は？ |
| 2021.05.19 | 各位（くらい）を求める | 1の位の値は？10の位は？ |
■広告
