黄金比とは

2020/03/23

数学

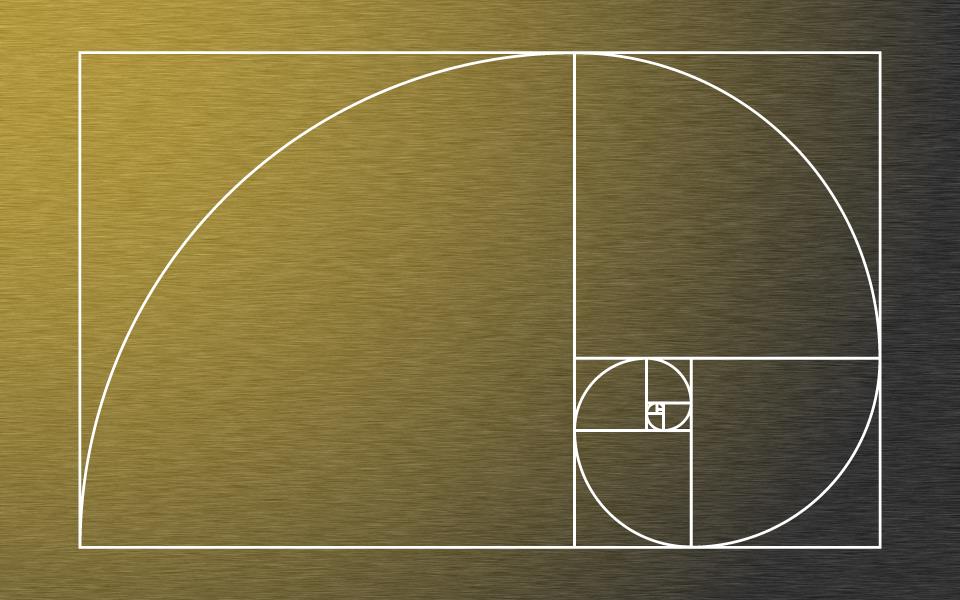
黄金比とは、人間が最も美しいと感じることができるとされている比率のことです。比率は以下のとおりです。

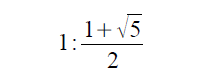
式を計算すると以下のような比率になります。1.618033…は、黄金数と呼ばれます。

この比率は、自然界で多く見られ、そしてデザインでも使われています。

自然界では、DNA、渦巻き（ハリケーン、銀河）、鉱物の結晶、ヒマワリの種の配列などにも黄金比が存在します。

デザインでは、モナ・リザ、ピラミッド、パルテノン神殿、ミロのビーナス、法隆寺五重塔、Apple社のロゴにも黄金比が使われています。

次に、この黄金比とフィボナッチ数列の関係について紹介します。

フィボナッチ数列は、イタリアの数学者レオナルド・フィボナッチが考えた「ウサギ算」から導かれる数列です。

それでは、フィボナッチ数列とはどうのようなものかを見ていきましょう。

n番目のフィボナッチ数をFnで表すと、Fnは再帰的に

　　F0 = 0

　　F1 = 1

　　Fn+2 = Fn + Fn+1　(n≧0)

で定義されます。

この式と黄金比との関係は、フィボナッチ数を１つ前のフィボナッチ数で割った値が黄金比に限りなく近づくというものです。

　　黄金比 = Fn / Fn-1

Javaソースコード

以下は、この関係をJavaのプログラムで確認したものです。

GoldenRatio1.java

ダウンロード

public class GoldenRatio1 {
	public static void main(String[] args) {
		double f0, f1, fn;
		double gr;	// 黄金比

		f0 = 0.0;
		f1 = 1.0;
		for ( int i = 2; i <= 1000; ++ i ) {
			fn = f0 + f1;
			// １つ前の値で、現値を割る
			gr = fn / f1;

			// 結果を表示
			if ( ( 20 >= i ) || ( 0 == ( i % 100 ) ) ) {
				System.out.println( i + ": " + gr );
			}

			// f0 ← f1、 f1 ← fn
			f0 = f1;
			f1 = fn;
		}
	}
}

実行結果

カウントダウンを実行

C:\talavax\javasample>java GoldenRatio1

出力結果

2: 1.0
3: 2.0
4: 1.5
5: 1.6666666666666667
6: 1.6
7: 1.625
8: 1.6153846153846154
9: 1.619047619047619
10: 1.6176470588235294
11: 1.6181818181818182
12: 1.6179775280898876
13: 1.6180555555555556
14: 1.6180257510729614
15: 1.6180371352785146
16: 1.618032786885246
17: 1.618034447821682
18: 1.6180338134001253
19: 1.618034055727554
20: 1.6180339631667064
100: 1.618033988749895
200: 1.618033988749895
300: 1.618033988749895
400: 1.618033988749895
500: 1.618033988749895
600: 1.618033988749895
700: 1.618033988749895
800: 1.618033988749895
900: 1.618033988749895
1000: 1.6180339887498951

計算結果が、黄金比に近づいていることが確認できました。

このプログラムでは、フィボナッチ数を1000まで求めて計算しています。この数を大きくしすぎるとオーバーフローが発生して正しい値が得られないので注意してください。